题目内容
设![]() 为实数,函数
为实数,函数![]() .
.
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 写出
写出![]() 的单调递减区间;
的单调递减区间;
(3)设函数![]()
![]() 且
且![]() 求不等式
求不等式![]() 的解集.
的解集.
(1)![]() (2)
(2)![]() 的单调递减区间
的单调递减区间![]()
(3)![]()
解析:
(1)若![]() ,则
,则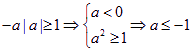
(2)当![]() 时,
时, ![]() 其对称轴
其对称轴![]() 则
则![]() 时
时![]() 单调递增
单调递增
当![]() 时,
时, ![]() 其对称轴
其对称轴![]() ,则
,则![]() 时
时![]() 单调递减
单调递减
所以:![]() 的单调递减区间
的单调递减区间![]()
(3):结合函数的图像与单调性,![]() 过
过![]() ,故在
,故在![]() 的条件下,当
的条件下,当![]() 时,
时,![]() 恒成立
恒成立
当![]() 时,
时,![]()
![]()
![]()
综上所述:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 为实数,函数
为实数,函数 。
。 ,求
,求 的最小值
的最小值  ,直接写出(不需要给出演算步骤)不等式
,直接写出(不需要给出演算步骤)不等式 的解集。
的解集。 为实数,函数
为实数,函数 。
。 的单调区间与极值;
的单调区间与极值; 且
且 时,
时, 。
。