题目内容
1)设函数![]() ,求
,求![]() 的最小值;
的最小值;
(2)设正数![]() 满足
满足![]() ,
,
求证![]()
(1)![]() 时取得最小值,
时取得最小值,![]() ;(2)同解析;
;(2)同解析;
解析:
(1)对函数![]() 求导数:
求导数:
![]()
![]()
![]()
于是![]()
当![]() 在区间
在区间![]() 是减函数,
是减函数,
当![]() 在区间
在区间![]() 是增函数.
是增函数.
所以![]() 时取得最小值,
时取得最小值,![]() ,
,
(Ⅱ)(i)当n=1时,由(Ⅰ)知命题成立.
(ii)假定当![]() 时命题成立,即若正数
时命题成立,即若正数![]() ,
,
则![]()
当![]() 时,若正数
时,若正数![]()
令![]()
则![]() 为正数,且
为正数,且![]()
由归纳假定知![]()
![]()
![]() ①
①
同理,由![]() 可得
可得![]()
![]() ②
②
综合①、②两式![]()
![]()
即当![]() 时命题也成立.
时命题也成立.
根据(i)、(ii)可知对一切正整数n命题成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,
, ·
· =
= ,
, ∈(0,
∈(0, ).
). 及
及 ,
, 的值;
的值; ,求
,求 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标; 上的值域.
上的值域.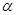 是第二象限角.
是第二象限角.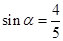 ,求
,求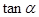 ,
,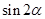 的值;
的值;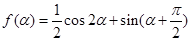 ,求
,求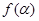 的最小值以及此时的角
的最小值以及此时的角