题目内容
设 ,
, ,
, ,
, 是某平面内的四个单位向量,其中
是某平面内的四个单位向量,其中 ,
, 与
与 的夹角为45°, 对这个平面内的任意一个向量
的夹角为45°, 对这个平面内的任意一个向量 ,规定经过一次“斜二测变换”得到向量
,规定经过一次“斜二测变换”得到向量 ,设向量
,设向量 是向量
是向量 经过一次“斜二测变换”得到的向量,则
经过一次“斜二测变换”得到的向量,则 是( )
是( )
| A.5 | B. | C.73 | D. |
A
解析试题分析:设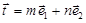 ,
, 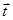 经过一次“斜二测变换”得到向量
经过一次“斜二测变换”得到向量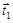 ,
,
则根据题意,可得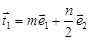 ,结合已知
,结合已知 ,得
,得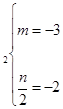 ,解之得
,解之得
m=-3,n=-4
∴向量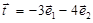 ,可得
,可得 ,故答案为:A
,故答案为:A
考点:平面向量数量积的运算;向量的模

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 是两个向量,
是两个向量,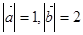 ,且
,且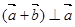 ,则
,则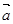 与
与 的夹角为( )
的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
已知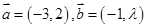 ,向量
,向量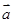 与
与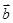 垂直,则实数
垂直,则实数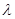 的值为( )
的值为( )
A.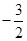 | B.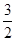 | C.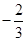 | D.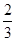 |
如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则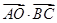 的值是(( )
的值是(( )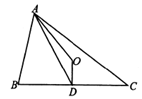
A.4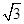 | B.8 | C.6 | D.6 |
若 ,
,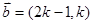 ,
, ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
已知三点A(1,1)、B(-1,0)、C(3,-1),则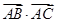 等于( )
等于( )
| A.-2 | B.-6 | C.2 | D.3 |
若两非零向量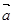 与
与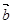 的夹角为
的夹角为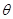 ,定义向量运算
,定义向量运算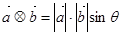 ,已知向量
,已知向量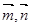 满足
满足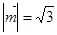 ,
,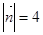 ,
,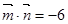 ,则
,则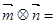 ( )
( )
| A.2 | B.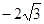 | C. | D.3 |
在△ABC中,AB=2,AC=3,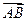 ·
·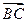 =1,则BC=( ).
=1,则BC=( ).
A. |
B.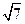 |
C.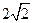 |
D.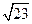 |



