题目内容

已知圆C1：(x+3)2+y2=1和圆C2：（x-3）2+y2=9,动圆M同时与圆C1及圆C2相外切，求动圆圆心M的轨迹方程.

x2-=1 (x≤-1)


解析:

如图所示，设动圆M与圆C1及圆C2分别外切于点A和点B，根据两圆外切的充要条件，得

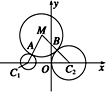|MC1|-|AC1|=|MA|，

|MC2|-|BC2|=|MB|.

因为|MA|=|MB|，

所以|MC2|-|MC1|=|BC2|-|AC1|=3-1=2.

这表明动点M到两定点C2，C1的距离之差是常数2.

根据双曲线的定义，动点M的轨迹为双曲线的左支（点M到C2的距离大，到C1的距离小），这里a=1,c=3,则b2=8,设点M的坐标为（x,y）,其轨迹方程为x2-=1 (x≤-1).

练习册系列答案
相关题目
在平面直角坐标系xoy中，已知圆C1：(x-1)2+y2=25和圆C2：(x-4)2+(y-5)2=16．
（1）若直线l1经过点P（2，-1）和圆C1的圆心，求直线l1的方程；
（2）若点P（2，-1）为圆C1的弦AB的中点，求直线AB的方程；
（3）若直线l过点A（6，0），且被圆C2截得的弦长为4
3
，求直线l的方程．
（2012•江苏一模）如图，在平面直角坐标系xOy中，已知圆C1：(x+1)2+y2=1，圆C2：(x-3)2+(y-4)2=1．
（1）若过点C1（-1，0）的直线l被圆C2截得的弦长为
65
，求直线l的方程；
（2）设动圆C同时平分圆C1的周长、圆C2的周长．
①证明：动圆圆心C在一条定直线上运动；
②动圆C是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．
已知圆C1：(x+3)2+y2=1和圆C2：(x-3)2+y2=9，动圆M同时与圆C1及圆C2外切，则动圆圆心M的轨迹方程为
x2-
y2
8
=1(x＜0)
x2-
y2
8
=1(x＜0)
．

在平面直角坐标系xOy中，已知圆C1：(x＋3)2＋(y－1)2＝4和圆C2：(x－4)2＋(y－5)2＝9.

(1)判断两圆的位置关系;

(2)求直线m的方程，使直线m被圆C1截得的弦长为4，与圆C截得的弦长是6.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网