��Ŀ����
��2012•����ģ�⣩��ͼ���ڱ߳�Ϊ4������ABCD�У���DAB=60�㣮��E��F�ֱ��ڱ�CD��CB�ϣ���E���C��D���غϣ�EF��AC��EF��AC=O����EF����CEF���۵���PEF��λ�ã�ʹƽ��PEF��ƽ��ABFED��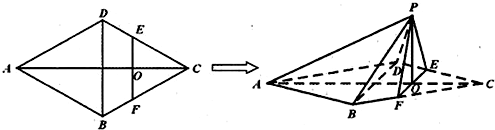
������֤��BD��ƽ��POA��
����PBȡ����Сֵʱ�������������⣺
��i��������P-BDEF�������
��ii������Q����
=��
���ˣ�0������̽����ֱ��OQ��ƽ��PBD���ɽǵĴ�С�Ƿ�һ������
����˵�����ɣ�

������֤��BD��ƽ��POA��
����PBȡ����Сֵʱ�������������⣺
��i��������P-BDEF�������
��ii������Q����
| AQ |
| QP |
| �� |
| 4 |
������������������ABCD�ĶԽ����ഹֱ֤��BD��AO��֤��PO��ƽ��ABFED���ɵ�PO��BD���������洹ֱ���ж����ɵ�BD��ƽ��POA��
�������ռ�ֱ������ϵO-xyz����������AO��BD=H��PO=x����
=
-
=�� 2
-x��2��-x�����Ӷ�ȷ��PB����Сֵ�������ɵ�����P-BDEF�������
������ȷ��
�����꣬���ƽ��PBD�ķ�����
=(1��0��1)�����������ļнǹ�ʽ����ֱ��OQ��ƽ��PBD���ɵĽǣ��Ӷ��ɵý��۳�����
�������ռ�ֱ������ϵO-xyz����������AO��BD=H��PO=x����
| PB |
| OB |
| OP |
| 3 |
������ȷ��
| OQ |
| n |
��� ����֤����������ABCD�ĶԽ����ഹֱ��
����֤����������ABCD�ĶԽ����ഹֱ��
��BD��AC����BD��AO��
��EF��AC����PO��EF��
��ƽ��PEF��ƽ��ABFED��ƽ��PEF��ƽ��ABFED=EF����PO?ƽ��PEF��
��PO��ƽ��ABFED��
��BD?ƽ��ABFED����PO��BD��
��AO��PO=O����BD��ƽ��POA������4�֣�
������ͼ����OΪԭ�㣬�����ռ�ֱ������ϵO-xyz����5�֣�
��������AO��BD=H����Ϊ��DAB=60�㣬���ԡ�BDCΪ�ȱ������Σ�
��BD=4��HB=2��HC=2
��
����PO=x����OH=2
-x��OA=4
-x��
����O��0��0��0����P��0��0��x����B��2
-x��2��0����
��
=
-
=�� 2
-x��2��-x������6�֣�
����|
|=
��
�൱x=
ʱ��|PB|min=
��
��ʱPO=
��OH=
��7�֣�
�ɣ���֪��PO��ƽ��ABFED������VP-BDEF=
(
��42-
��22)��
=3����8�֣�
���������Q������Ϊ��a��0��c�����ɣ�i��֪��OP=
����A��3
��0��0����B��
��2��0����D��
��-2��0����P��0��0��
����
����
=(a-3
��0��c)��
=(-a��0��
-c)����9�֣�
��
=��
���ˣ�0����
��
����
��
��Q��
��
����
��
=��
��0��
���� ��10�֣�
��ƽ��PBD�ķ�����Ϊ
=(x��y��z)����
•
=0��
•
=0��
��
=(
��2��-
)��
=(0��-4��0)����
��
ȡx=1����ã�y=0��z=1������
=(1��0��1)����11�֣�
��ֱ��OQ��ƽ��PBD���ɵĽǦȣ�
��sin��=|cos��
��
��|=
=
��
����12�֣�
�֡ߦˣ�0��sin�ȣ�
����13�֣�
�ߦȡ�[0��
]����ȣ�
��
���ֱ��OQ��ƽ��PBD���ɽǴ���
�������۳����� ��14�֣�
 ����֤����������ABCD�ĶԽ����ഹֱ��
����֤����������ABCD�ĶԽ����ഹֱ����BD��AC����BD��AO��
��EF��AC����PO��EF��
��ƽ��PEF��ƽ��ABFED��ƽ��PEF��ƽ��ABFED=EF����PO?ƽ��PEF��
��PO��ƽ��ABFED��
��BD?ƽ��ABFED����PO��BD��
��AO��PO=O����BD��ƽ��POA������4�֣�
������ͼ����OΪԭ�㣬�����ռ�ֱ������ϵO-xyz����5�֣�
��������AO��BD=H����Ϊ��DAB=60�㣬���ԡ�BDCΪ�ȱ������Σ�
��BD=4��HB=2��HC=2
| 3 |
����PO=x����OH=2
| 3 |
| 3 |
����O��0��0��0����P��0��0��x����B��2
| 3 |
��
| PB |
| OB |
| OP |
| 3 |
����|
| PB |
2(x-
|
�൱x=
| 3 |
| 10 |
��ʱPO=
| 3 |
| 3 |
�ɣ���֪��PO��ƽ��ABFED������VP-BDEF=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 4 |
| 3 |
���������Q������Ϊ��a��0��c�����ɣ�i��֪��OP=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
����
| AQ |
| 3 |
| QP |
| 3 |
��
| AQ |
| QP |
��
|
|
��Q��
3
| ||
| ��+1 |
| ||
| ��+1 |
��
| OQ |
3
| ||
| ��+1 |
| ||
| ��+1 |
��ƽ��PBD�ķ�����Ϊ
| n |
| n |
| PB |
| n |
| BD |
��
| PB |
| 3 |
| 3 |
| BD |
|
ȡx=1����ã�y=0��z=1������
| n |
��ֱ��OQ��ƽ��PBD���ɵĽǦȣ�
��sin��=|cos��
| OQ |
| n |
| |3+��| | ||||
|
| 1 | ||
|
1+
|
�֡ߦˣ�0��sin�ȣ�
| ||
| 2 |
�ߦȡ�[0��
| �� |
| 2 |
| �� |
| 4 |
���ֱ��OQ��ƽ��PBD���ɽǴ���
| �� |
| 4 |
���������⿼�����洹ֱ����������ǣ��������ÿռ�����������弸�����⣬ȷ��ƽ��ķ������ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
