题目内容
已知函数 是R上的奇函数,若对于
是R上的奇函数,若对于 ,都有
,都有 ,
, 时,
时, 的值为( )
的值为( )
A. | B. | C.1 | D.2 |
C
解析试题分析:根据题意,由于函数是奇函数,且满足f(x+2)=f(x),则说明周期为2,同时利用 时,
时, 的值为f(1)+f(0)=1,故可知结论为1,故选C.
的值为f(1)+f(0)=1,故可知结论为1,故选C.
考点:函数的奇偶性
点评:主要是考查了函数的奇偶性以及解析式 运用,属于基础题。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
下列函数中既是偶函数,又在区间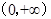 上单调递增的函数是( )
上单调递增的函数是( )
A.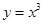 | B.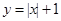 | C.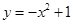 | D.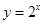 |
定义在区间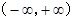 上的奇函数
上的奇函数 为增函数,偶函数
为增函数,偶函数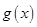 在
在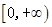 上图象与
上图象与 的图象重合.设
的图象重合.设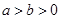 ,给出下列不等式,其中成立的是( )
,给出下列不等式,其中成立的是( )
①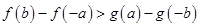
②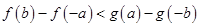
③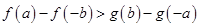
④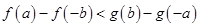
| A.①④ | B.②③ | C.①③ | D.②④ |
设函数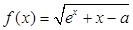 (
(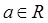 ,
,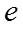 为自然对数的底数).若存在
为自然对数的底数).若存在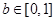 使
使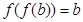 成立,则
成立,则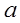 的取值范围是
的取值范围是
A.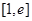 | B.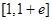 | C.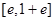 | D.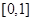 |
方程 有唯一解,则实数
有唯一解,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. 或 或 | D. 或 或 或 或 |
设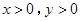 ,定义
,定义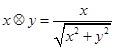 ,则
,则 +2
+2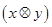
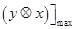 等于( )
等于( )
A.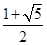 | B.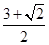 |
C.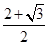 | D.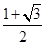 |
下列函数中,周期是 且在
且在 上为增函数的是( )
上为增函数的是( )
A. | B. | C. | D. |
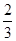
 (x∈R)满足
(x∈R)满足 ,
, ,则
,则 的图象可能是
的图象可能是