题目内容
有3个命题
(1)底面是正三角形,其余各个面都是等腰三角形的棱锥是正三棱锥;
(2)各个侧面都是等腰三角形的四棱锥是正四棱锥;
(3)底面是正三角形,相邻两侧面所成的二面角都相等的三棱锥是正三棱锥.
其中假命题的个数是( )
(1)底面是正三角形,其余各个面都是等腰三角形的棱锥是正三棱锥;
(2)各个侧面都是等腰三角形的四棱锥是正四棱锥;
(3)底面是正三角形,相邻两侧面所成的二面角都相等的三棱锥是正三棱锥.
其中假命题的个数是( )
分析:根据正棱锥的结构特征,底面是正多边形,顶点在底面的射影是底面多边形的中心,依次分析4个命题:对于(1),存在反例,可得(1)错误,对于(2)不符合底面必须是正方形,也错误;对于(3)凡是顶点在底面过正三角形的中心的垂线上的三棱锥都满足条件,但不一定都是正三棱锥,错误.综合可得答案.
解答: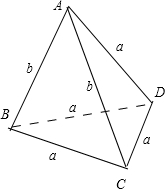 解:(1)、如图:三棱锥A-BCD中,AB=AC=b,AD=CD=BC=BD=a,
解:(1)、如图:三棱锥A-BCD中,AB=AC=b,AD=CD=BC=BD=a,
其每个侧面是等腰三角形,但不是正三棱锥,故(1)错误;
(2)底面是棱形但不是正方形的四棱锥的各个侧面有可能都是等腰三角形,
故各个侧面都是等腰三角形的四棱锥不一定是正四棱锥,故(2)错误;
(3)凡是顶点在底面过正三角形的中心的垂线上的三棱锥都满足
底面是正三角形,相邻两侧面所成的二面角都相等,但不一定都是正三棱锥,故(3)错误.
故选D.
 解:(1)、如图:三棱锥A-BCD中,AB=AC=b,AD=CD=BC=BD=a,
解:(1)、如图:三棱锥A-BCD中,AB=AC=b,AD=CD=BC=BD=a,其每个侧面是等腰三角形,但不是正三棱锥,故(1)错误;
(2)底面是棱形但不是正方形的四棱锥的各个侧面有可能都是等腰三角形,
故各个侧面都是等腰三角形的四棱锥不一定是正四棱锥,故(2)错误;
(3)凡是顶点在底面过正三角形的中心的垂线上的三棱锥都满足
底面是正三角形,相邻两侧面所成的二面角都相等,但不一定都是正三棱锥,故(3)错误.
故选D.
点评:本题考查正棱锥的概念的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目