题目内容
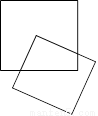
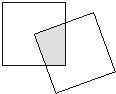 现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为| a2 |
| 4 |
分析:首先平面正方形的知识可知一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
,结合空间正方体的结构特征,即可类比推理出两个两个正方体重叠部分的体积.
| a2 |
| 4 |
解答:解:∵同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,
则这两个正方形重叠部分的面积恒为
,
类比到空间有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,
则这两个正方体重叠部分的体积恒为
,
故选C
则这两个正方形重叠部分的面积恒为
| a2 |
| 4 |
类比到空间有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,
则这两个正方体重叠部分的体积恒为
| a3 |
| 8 |
故选C
点评:本题考查类比推理,解答本题的关键是根据平面中正方形的性质类比推理出空间正方体的性质特征,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
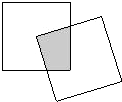 现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___
,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___
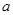 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ,类比到空间,有两个棱长均为
,类比到空间,有两个棱长均为
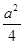 ,类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 ;
,类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 ;