Question

下列关于圆锥曲线的命题：其中真命题的序号    ．（写出所有真命题的序号）．
①设A，B为两个定点，若|PA|-|PB|=2，则动点P的轨迹为双曲线；
②设A，B为两个定点，若动点P满足|PA|=10-|PB|，且|AB|=6，则|PA|的最大值为8；
③方程2x²-5x+2=0的两根可分别作椭圆和双曲线的离心率；
④双曲线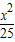-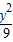=1与椭圆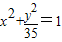有相同的焦点．

Answer 1

【答案】分析：①利用双曲线的定义判断．②利用椭圆的定义判断．③利用椭圆和双曲线的离心率的取值范围判断．④利用双曲线和椭圆的方程和定义判断．
解答：解：①根据双曲线的定义可知，满足|PA|-|PB|=2的动点P不一定是双曲线，这与AB的距离有关系，所以①错误．
②由|PA|=10-|PB|，得|PA|+|PB|=10＞|AB|，所以动点P的轨迹为以A，B为焦点的图象，且2a=10，2c=6，所以a=5，c=3，根据椭圆的性质可知，|PA|的最大值为a+c=5+3=8，所以②正确．
③方程2x²-5x+2=0的两个根为x=2或x=，所以方程2x²-5x+2=0的两根可分别作椭圆和双曲线的离心率，所以③正确．
④由双曲线的方程可知，双曲线的焦点在x轴上，而椭圆的焦点在y轴上，所以它们的焦点不可能相同，所以④错误．
故正确的命题为②③．
故答案为：②③．
点评：本题主要考查圆锥曲线的定义和性质，要求熟练掌握圆锥曲线的定义，方程和性质．