题目内容
某试验田分别种植了甲乙两种水稻,为了研究这两种水稻的产量,抽检了甲、乙两种水稻的谷穗各1000株.经统计,得到每株谷穗的粒数的频率分布直方图如图:

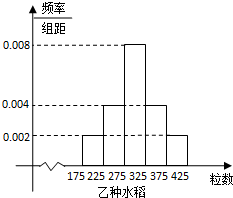
(Ⅰ)求乙种水稻谷穗的粒数落在[325,375)之间的频率,并将频率分布直方图补齐;
(Ⅱ)试根据频率分布直方图估计甲种水稻谷穗粒数的中位数与平均数(精确到0.1);
(Ⅲ)根据频率分布直方图,请至少从两方面对甲乙两种水稻谷穗的粒数作出评价.

(Ⅰ)求乙种水稻谷穗的粒数落在[325,375)之间的频率,并将频率分布直方图补齐;
(Ⅱ)试根据频率分布直方图估计甲种水稻谷穗粒数的中位数与平均数(精确到0.1);
(Ⅲ)根据频率分布直方图,请至少从两方面对甲乙两种水稻谷穗的粒数作出评价.
分析:(I)根据频率分布直方图的小矩形的面积和为1,可求落在[325,375)内的频率,利用组距为50,求出小矩形的高;
(II)根据中位数的左右两边小矩形的面积和相等,求得从左开始面积和为0.5的小矩形底边横坐标值,即为中位数;计算各个小矩形的底边中间值乘以其面积之和,即为数据的平均数;
(III)根据甲、乙两种水稻谷粒的平均数大小和频率分布情况说明.
(II)根据中位数的左右两边小矩形的面积和相等,求得从左开始面积和为0.5的小矩形底边横坐标值,即为中位数;计算各个小矩形的底边中间值乘以其面积之和,即为数据的平均数;
(III)根据甲、乙两种水稻谷粒的平均数大小和频率分布情况说明.
解答:解:(Ⅰ)乙种水稻谷穗的粒数落在[325,375)之间的频率为1-50×(0.002+0.004+0.008+0.002)=0.2,
频率分布直方图如图所示.
(Ⅱ)设中位数估计值为x,则有 50×(0.004+0.002)+(x-275)×0.006=0.5,解得x=308.3
由直方图得平均数的估计值为50×0.004×200+50×0.002×250+50×0.006×300+50×0.003×350+50×0.005×400=307.5,
答:中位数和平均数的估计值分别为308.3和307.5,
(Ⅲ)由于乙稻谷谷穗粒数平均值的估计值为300<307.5
故可得出结论:乙稻谷谷穗粒数总体上少于甲种水稻,又从频率分布直方图可看出乙稻谷谷穗粒数比甲种水稻要整齐.
频率分布直方图如图所示.

(Ⅱ)设中位数估计值为x,则有 50×(0.004+0.002)+(x-275)×0.006=0.5,解得x=308.3
由直方图得平均数的估计值为50×0.004×200+50×0.002×250+50×0.006×300+50×0.003×350+50×0.005×400=307.5,
答:中位数和平均数的估计值分别为308.3和307.5,
(Ⅲ)由于乙稻谷谷穗粒数平均值的估计值为300<307.5
故可得出结论:乙稻谷谷穗粒数总体上少于甲种水稻,又从频率分布直方图可看出乙稻谷谷穗粒数比甲种水稻要整齐.
点评:本题考查了利用频率分布直方图求中位数、平均数,考查了学生搜集信息分析问题、解决问题的能力,解答的关键是读懂频率分布直方图的数据.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目