Question

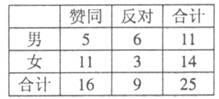
某媒体对“男女同龄退休”这一公众关注的问题进行 了民意调査，右表是在某单位得到的数据（人数）：

	赞同	反对	合计
男	5	6	11
女	11	3	14
合计	16	9	25

（1 ）能否有90%以上的把握认为对这一问题的看法与性别有关？
（2）进一步调查：（ⅰ）从赞同“男女同龄退休”16人中选出3人进行陈述发言，求事件“男士和女士各至少有1人发言”的概率；
（ⅱ）从反对“男女同龄退休”的9人中选出3人进行座谈，设参加调査的女士人数为X，求X的分布列和期望．
附表：

P（K2≥K）	0.25	0.15	0.10
k	1.323	2.072	2.706

K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

．

Answer 1

分析：（1）由题设知K²=

25×(5×3-6×11)2

16×9×11×14

≈2.932＞2.706，由此得到结果．
（2）（i）记题设事件为A，利用组合数公式得P（A）=

C 1 5 C 2 11 + C 2 5 C 1 11

C 3 16

，由此能求出事件“男士和女士各至少有1人发言”的概率．
（ii）根据题意，X服从超几何分布，P（X=k）=

C k 3 C 3-k 6

C 3 9

，k=0，1，2，3．由此能求出X的分布列和期望．

解答：解：（1）K²=

25×(5×3-6×11)2

16×9×11×14

≈2.932＞2.706，
由此可知，有90%的把握认为对这一问题的看法与性别有关．…（3分）
（2）（ⅰ）记题设事件为A，则
所求概率为P（A）=

C 1 5 C 2 11 + C 2 5 C 1 11

C 3 16

=

11

16

．    …（7分）
（ⅱ）根据题意，X服从超几何分布，P（X=k）=

C k 3 C 3-k 6

C 3 9

，k=0，1，2，3．
X的分布列为

X	0	1	2	3
P	5 21	15 28	3 14	1 84

…（10分）
X的期望E（X）=0×

5

21

+1×

15

28

+2×

3

14

+3×

1

84

=1．   …（12分）

点评：考查独立性检验、互斥事件的概率、超几何分布、分布列、期望，以及分析解决实际问题的能力．