题目内容
已知动圆过定点A(1,0),且与直线x=-1相切.
(1)求动圆的圆心轨迹C的方程;
(2)若直线l过点A,并与轨迹C交于P,Q两点,且满足
=3
,求直线l的方程.
(1)求动圆的圆心轨迹C的方程;
(2)若直线l过点A,并与轨迹C交于P,Q两点,且满足
| PA |
| AQ |
(1)∵动圆过定点A(1,0),且与直线x=-1相切,
∴曲线C是以点A为焦点,直线x=-1为准线的抛物线,其方程为y2=4x.
(2)由题意直线的斜率存在,设方程为:y=k(x-1),代入抛物线方程,整理得k2x2-(2k2+4)x+k2=0
设P(x1,y1),Q(x2,y2)
∵
=3
,∴
∴x1=3,x2=
∴3+
=
∴k=±
∴直线l的方程为y=±
(x-1).
∴曲线C是以点A为焦点,直线x=-1为准线的抛物线,其方程为y2=4x.
(2)由题意直线的斜率存在,设方程为:y=k(x-1),代入抛物线方程,整理得k2x2-(2k2+4)x+k2=0
设P(x1,y1),Q(x2,y2)
∵
| PA |
| AQ |
|
∴x1=3,x2=
| 1 |
| 3 |
∴3+
| 1 |
| 3 |
| 2k2+4 |
| k2 |
∴k=±
| 3 |
∴直线l的方程为y=±
| 3 |

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
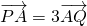 ,求直线l的方程.
,求直线l的方程.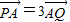 ,求直线l的方程.
,求直线l的方程.