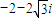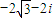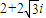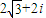题目内容
设复数z的幅角的主值为
,虚部为
,则z2=( )
| 2π |
| 3 |
| 3 |
A、-2-2
| ||
B、-2
| ||
C、2+2
| ||
D、2
|
分析:将复数设为三角形式,据虚部为
求出复数的模,求出复数的三角形式,利用棣莫弗定理求出z2
| 3 |
解答:解:∵复数z的幅角的主值为
设复数z=r(cos
+isin
)=-
r+
r
∵虚部为
∴
r=
∴r=2
∴z=2(cos
+isin
)
∴z2=4(cos
+isin
)=-2-2
i
故选项为A
| 2π |
| 3 |
设复数z=r(cos
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∵虚部为
| 3 |
∴
| ||
| 2 |
| 3 |
∴r=2
∴z=2(cos
| 2π |
| 3 |
| 2π |
| 3 |
∴z2=4(cos
| 4π |
| 3 |
| 4π |
| 3 |
| 3 |
故选项为A
点评:本题考查复数的三角形式与代数形式及复数的棣莫弗定理.

练习册系列答案
相关题目
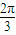 ,虚部为
,虚部为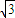 ,则z2=( )
,则z2=( )
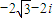
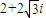
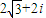
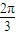 ,虚部为
,虚部为 ,则z2=( )
,则z2=( )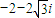
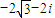
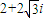
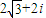
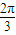 ,虚部为
,虚部为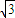 ,则z2=( )
,则z2=( )