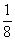题目内容
已知0＜k＜
，直线l1：kx-y-k+1=0，l2：x-ky+2k=0的交点在
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
B
分析：解方程组得两直线的交点坐标，由0＜k＜，求出交点的横坐标、纵坐标的符号，得出结论．
解答：解方程组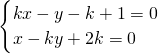
得，两直线的交点坐标为（
，
），
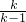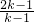因为0＜k＜，
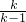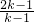所以，＜0，＞0，
所以交点在第二象限．
故选B．
点评：本题考查求两直线的交点的方法，以及各个象限内的点的坐标的特征，考查计算能力．
分析：解方程组得两直线的交点坐标，由0＜k＜
，求出交点的横坐标、纵坐标的符号，得出结论．解答：解方程组
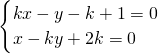得，两直线的交点坐标为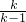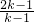（，），因为0＜k＜
，所以，
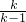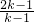＜0，＞0，所以交点在第二象限．
故选B．
点评：本题考查求两直线的交点的方法，以及各个象限内的点的坐标的特征，考查计算能力．
练习册系列答案
53随堂测系列答案
相关题目
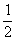C.
D.
C.
D.