题目内容
下列说法:①用“辗转相除法”求得243,135 的最大公约数是9;
②命题p:?x∈R,x2-x+
| 1 |
| 4 |
| 1 |
| 4 |
③已知条件p:x>1,y>1,条件q:x+y>2,xy>1,则条件p是条件q成立的充分不必要条件;
④若
| a |
| b |
| a |
| b |
| π |
| 2 |
⑤已知f(n)=
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
⑥直线l:y=kx+1与双曲线C:x2-y2=1的左支有且仅有一个公共点,则k的取值范围是-1<k<1或k=
| 2 |
其中正确的命题的序号为
分析:根据最大公约数的定义及辗转相除法的运算规则,我们可以求出243,135 的最大公约数,判断①的真假;根据全称命题的否定方法,写出命题非p,可以判断出②的真假;根据充要条件的定义,我们可以判断③的真假;根据向量垂直的充要条件,我们易判断
⊥
,进而得到④的真假;根据已知中f(n)的表达式从n开始,到n2结束,我们易确定f(n)的项数,进而判断⑤的真假,根据直线与双曲线只有一个交点时,直线与双曲线左支相切,或夹在两条渐近线之间,我们易求出k的取值范围,进而判断⑥的真假,进而得到答案.
| a |
| b |
解答:解:用“辗转相除法”求得243,135 的最大公约数是27,故①错误;
命题p:?x∈R,x2-x+
<0,则?p是?x0∈R,x02-x0+
≥0,故②正确;
已知条件p:x>1,y>1,条件q:x+y>2,xy>1,则条件p是条件q成立的充分不必要条件,故③正确;
若
=(1,0,1),
=(-1,1,0),
•
=0,即
⊥
,则<
,
>=
,故④正确;
已知f(n)=
+
+
+…+
,则f(n)中共有n2-n+1项,当n=2时,f(2)=
+
+
,故⑤正确;
直线l:y=kx+1与双曲线C:x2-y2=1的左支有且仅有一个公共点,则k的取值范围是-1<k≤1或k=
,故⑥错误.
故答案为:②③④⑤
命题p:?x∈R,x2-x+
| 1 |
| 4 |
| 1 |
| 4 |
已知条件p:x>1,y>1,条件q:x+y>2,xy>1,则条件p是条件q成立的充分不必要条件,故③正确;
若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 2 |
已知f(n)=
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
直线l:y=kx+1与双曲线C:x2-y2=1的左支有且仅有一个公共点,则k的取值范围是-1<k≤1或k=
| 2 |
故答案为:②③④⑤
点评:本题的考查的知识点是命题的真假判断与应用,直线与圆锥曲线的关系,空间向量的夹角与距离,辗转相除法,熟练掌握这些基本知识点,并逐一判断题目中各命题的真假是解答本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
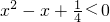 ,则?p是
,则?p是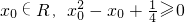 ;
;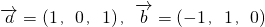 ,则
,则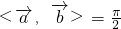 ;
;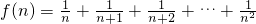 ,则f(n)中共有n2-n+1项,当n=2时,
,则f(n)中共有n2-n+1项,当n=2时,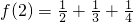 ;
;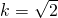 .
. ,则¬p是
,则¬p是 ;
; ,则
,则 ;
; ,则f(n)中共有n2-n+1项,当n=2时,
,则f(n)中共有n2-n+1项,当n=2时, ;
; .
.