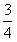题目内容
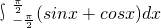的值为
- A.0
- B.
- C.2
- D.4
C
分析：本题考查的知识点是简单复合函数的定积分，要求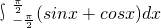，关键是要确定满足条件F′（x）=sinx+cosx的函数F（x），根据三角函数的导数的公式，我们易得F（x）=-cosx+sinx，代入即可求出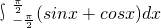的值．
解答：令F（x）=-cosx+sinx，
∴F′（x）=sinx+cosx，
所以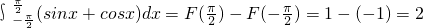
．
故选C
点评：解答定积分的计算题，关键是熟练掌握定积分的相关性质：①∫ab1dx=b-a②∫abkf（x）dx=k∫abf（x）dx③∫abf（x）±g（x）dx=∫abf（x）dx±∫abg（x）dx
分析：本题考查的知识点是简单复合函数的定积分，要求
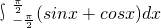，关键是要确定满足条件F′（x）=sinx+cosx的函数F（x），根据三角函数的导数的公式，我们易得F（x）=-cosx+sinx，代入即可求出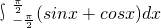的值．解答：令F（x）=-cosx+sinx，
∴F′（x）=sinx+cosx，
所以
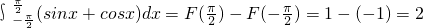．故选C
点评：解答定积分的计算题，关键是熟练掌握定积分的相关性质：①∫ab1dx=b-a②∫abkf（x）dx=k∫abf（x）dx③∫abf（x）±g（x）dx=∫abf（x）dx±∫abg（x）dx
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，则
的值为
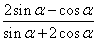＜x≤2}．若A=B，则a的值为
的值为
