题目内容
与普通方程x2+y-1=0等价的参数方程是
A.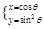 (θ为参数) (θ为参数) | B.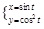 (t为参数) (t为参数) |
C.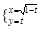 (t为参数) (t为参数) | D.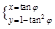 (φ为参数) (φ为参数) |
D
解析试题分析:选项A中,由于普通方程x2+y-1=0中x可以取得一切实数,因此可知A中x大于等于-1,小于等于1,故错误。
选项B中,同理可知结合正弦函数的有界性可知x不是取得一切实数,错误
选项C中,由于偶次根式的定义可知 ,x
,x 0不可取得一切实数,不成立。
0不可取得一切实数,不成立。
选项D中,结合正切函数图像可知,满足题意故成立。选D
考点:本题主要考查了普通方程与参数方程的互化问题的运用。
点评:解决该试题的关键是注意到不同参数中变量的限定范围,以及消去参数的思想的得到普通方程的一般思路。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线的参数方程为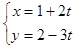 (
( 为参数),则直线的斜率为( )
为参数),则直线的斜率为( )
A.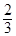 | B.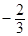 | C. | D.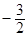 |
曲线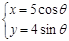 (
(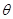 为参数)的焦距是 ( )
为参数)的焦距是 ( )
| A.3 | B.6 | C.8 | D.10 |
若直线的参数方程为 ,则直线的斜率为( )
,则直线的斜率为( )
A.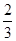 | B.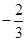 | C.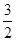 | D. |
在方程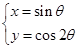 (q为参数)表示的曲线上的一个点的坐标是( )
(q为参数)表示的曲线上的一个点的坐标是( )
| A.(2,-7) | B.(1,0) | C.(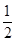 , ,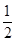 ) ) | D.(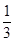 , ,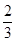 ) ) |
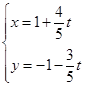 (
( 为参数)被曲线
为参数)被曲线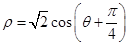 所截得的弦长为 .
所截得的弦长为 . 中,直线
中,直线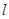 的参数方程为
的参数方程为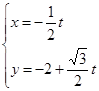 (
(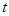 为参数),以原点
为参数),以原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为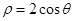 ,则
,则 与
与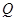 间的最短距离为 .
间的最短距离为 .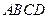 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心,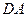 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长.
 (
( 为参数)的普通方程为___________.
为参数)的普通方程为___________.