题目内容
直线y=2x+1关于y轴对称的直线方程为
| A.y=-2x+1 | B.y=2x-1 | C.y=-2x-1 | D.y=-x-1 |
A
解析试题分析:直线y=2x+1斜率为2,与y轴相交于点 ,与之对称的直线斜率为
,与之对称的直线斜率为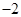 ,所以所求直线为y=-2x+1
,所以所求直线为y=-2x+1
考点:直线间的对称
点评:求直线关于直线的对称直线,可从已知直线上任取2点,找到这两点的对称点,再由两点求直线

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
动点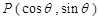
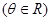 关于直线
关于直线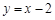 的对称点是
的对称点是 ,则
,则 的最大值为( )
的最大值为( )
A. | B.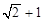 | C.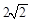 | D.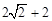 |
如图,若图中直线 1,
1,  2,
2,  3的斜率分别为k1, k2, k3,则
3的斜率分别为k1, k2, k3,则
| A.k1<k2<k3 | B.k3<k1<k2 | C.k3<k2<k1 | D.k1<k3<k2 |
如果直线(3a+2)x+ay-1=0与直线2ax+y-2a+1=0互相平行,则实数a的值为 ( )
A.0或- | B.- | C.2 | D.2或- |
直线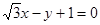 的倾斜角是( )
的倾斜角是( )
| A.30° | B.60° | C.120° | D.150° |
已知直线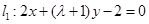 ,
, ,若
,若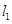 ∥
∥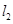 ,则
,则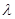 的值是( )
的值是( )
A.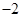 | B. | C.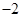 或1 或1 | D.1 |
直线 的倾斜角的正切值为-
的倾斜角的正切值为- ,直线
,直线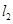 与
与 垂直,则
垂直,则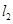 的斜率是( )
的斜率是( )
A. | B. | C.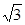 | D. |
已知直线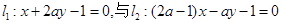 平行,则
平行,则 的值是( )
的值是( )
| A.0或1 | B.1或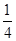 | C.0或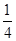 | D.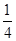 |
过点(1,0)且与直线x-2y-2=0平行的直线方程是( )
| A.x-2y-1=0 | B.x-2y+1="0" | C.2x+y-2=0 | D.x+2y-1=0 |