题目内容
已知抛物线y2=2px(p>0)的焦点F与双曲线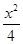 -
-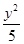 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|= |AF|,则A点的横坐标为( )
|AF|,则A点的横坐标为( )
A.2 | B.3 | C.2 | D.4 |
B
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线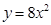 的焦点坐标为( )
的焦点坐标为( )
A. | B.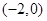 | C. | D. |
过抛物线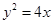 焦点
焦点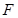 的直线交其于
的直线交其于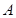 ,
,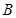 两点,
两点,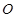 为坐标原点.若
为坐标原点.若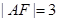 ,则
,则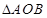 的面积为( )
的面积为( )
A.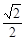 | B.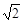 | C.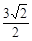 | D.2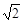 |
过双曲线 -
- =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
| A.x±y=0 | B.2x±y=0 |
| C.4x±y=0 | D.x±2y=0 |
在抛物线y=x2+ax-5(a≠0)上取横坐标为x1=-4,x2=2的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆5x2+5y2=36相切,则抛物线顶点的坐标为( )
| A.(-2,-9) | B.(0,-5) |
| C.(2,-9) | D.(1,-6) |
已知抛物线x2=4y上有一条长为6的动弦AB,则AB中点到x轴的最短距离为( )
A. | B. | C.1 | D.2 |
若已知点Q(4,0)和抛物线y= x2+2上一动点P(x,y),则y+|PQ|最小值为( )
x2+2上一动点P(x,y),则y+|PQ|最小值为( )
A.2+2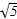 | B.11 | C.1+2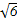 | D.6 |
 (B)
(B) (C)
(C) (D)
(D)
