题目内容
经过点P(1,4)的直线在两坐标轴上的截距都是正值,且截距之和最小,则直线的方程为( )
| A、x+2y-6=0 | B、2x+y-6=0 | C、x-2y+7=0 | D、x-2y-7=0 |
分析:设出直线方程的截距式,把经过的点P(1,4)的坐标代入得a与b的等式关系,把截距的和a+b变形后使用基本不等式求出它的最小值.
解答:解:设直线的方程为
+
=1(a>0,b>0),则有
+
=1,
∴a+b=(a+b)×1=(a+b)×(
+
)=5+
+
≥5+4=9,
当且仅当
=
,即a=3,b=6时取“=”.
∴直线方程为2x+y-6=0.
故选B.
| x |
| a |
| y |
| b |
| 1 |
| a |
| 4 |
| b |
∴a+b=(a+b)×1=(a+b)×(
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
当且仅当
| b |
| a |
| 4a |
| b |
∴直线方程为2x+y-6=0.
故选B.
点评:本题考查直线方程的截距式,利用基本不等式求截距和的最小值,注意等号成立的条件需检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有共同的渐近线,且经过点P(1,4)的双曲线方程为( )[来源:学_科_网Z_X_X_K]
有共同的渐近线,且经过点P(1,4)的双曲线方程为( )[来源:学_科_网Z_X_X_K] B.
B.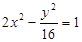 C.
C. D.
D.
 有共同的渐近线,且经过点P(1,4)的双曲线方程为 ( )
有共同的渐近线,且经过点P(1,4)的双曲线方程为 ( ) B.
B. C.
C. D.
D.