题目内容

（2012•三明模拟）在Rt△PAB中，PA=PB，点C、D分别在PA、PB上，且CD∥AB，AB=3，AC=
2
，则
AD
•
BC
的值为（　　）
分析：建立直角坐标系，根据条件写出A，B，C，D的坐标，然后求出向量的坐标，代入向量的数量积的坐标表示即可求解
解答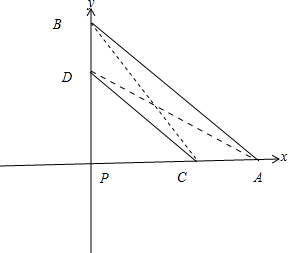：解：建立如图所示的直角坐标系，
∵PA=PB，CD∥AB，AB=3，AC=
2

∴PA=PB=
3
2
2
，PC=
2
2

∴A（
3
2
2
，0），B（0，
3
2
2
）C（
2
2
，0）D（0，
2
2
）
∴
AD
=（-
3
2
2
，
2
2
），
BC
=（
2
2
，-
3
2
2
）
∴
AD
•
BC
=-
3
2
2
×
2
2
-
2
2
×
3
2
2
=-3
故选C
点评：本题主要考查了向量的数量积的求解，解题的关键是建立坐标系，把所求问题坐标化
练习册系列答案
相关题目
（2012•三明模拟）某食品厂对生产的某种食品按行业标准分成五个不同等级，等级系数X依次为A，B，C，D，E．现从该种食品中随机抽取20件样品进行检验，对其等级系数进行统计分析，得到频率分布表如下：
X A B C D E
频率 a 0.2 0.45 b c
（Ⅰ）在所抽取的20件样品中，等级系数为D的恰有3件，等级系数为E的恰有2件，求a，b，c的值；
（Ⅱ）在（Ⅰ）的条件下，将等级系数为D的3件样品记为x1，x2，x3，等级系数为E的2件样品记为y1，y2，现从x1，x2，x3，y1，y2这5件样品中一次性任取两件（假定每件样品被取出的可能性相同），试写出所有可能的结果，并求取出的两件样品是同一等级的概率．
（2012•三明模拟）已知集合M={x|-1≤x≤1}，N={0，1，2}，则M∩N为（　　）
（2012•三明模拟）已知正实数a，b满足不等式ab+1＜a+b，则函数f（x）=loga（x+b）的图象可能为（　　）
（2012•三明模拟）已知函数f（x）=x（x-a）2，a是大于零的常数．
（Ⅰ）当a=1时，求f（x）的极值；
（Ⅱ）若函数f（x）在区间[1，2]上为单调递增，求实数a的取值范围；
（Ⅲ）证明：曲线y=f（x）上存在一点P，使得曲线y=f（x）上总有两点M，N，且
MP
=
PN
成立．
（2012•三明模拟）若a∈[0，3]，则函数f（x）=x2-2ax+a有零点的概率为
2
3
2
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网