题目内容
设A、B、C三个事件相互独立,事件A发生的概率是 ,A、B、C中只有一个发生的概率是
,A、B、C中只有一个发生的概率是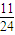 ,又A、B、C中只有一个不发生的概率是
,又A、B、C中只有一个不发生的概率是 .
.(1)求事件B发生的概率及事件C发生的概率;
(2)试求A、B、C均不发生的概率.
【答案】分析:(1)先设出事件A,B,C发生的概率,用其表示A、B、C中只有一个发生的概率,A、B、C中只有一个不发生的概率,化简,即可计算出事件B,C发生的概率.
(2)用对立事件的概率分别求出A、B、C各自不发生的概率,再相乘即可.
解答:解:(1)设事件A发生的概率为P(A),事件B发生的概率为P(B),事件C发生的概率为P(C),
则P(A)= ,
,
P(A )+P(
)+P( C)+P(
C)+P( )=P(A)(1-P(B))(1-P(C))+(1-P(A))(1-P(B))P(C)+(1-P(A))P(B)(1-P(C))=
)=P(A)(1-P(B))(1-P(C))+(1-P(A))(1-P(B))P(C)+(1-P(A))P(B)(1-P(C))= ,
,
P(AB )+P(A
)+P(A C)+P(
C)+P( BC)=P(A)P(B)(1-P(C))+P(A)(1-P(B))P(C)+(1-P(A)P(B)P(C)=
BC)=P(A)P(B)(1-P(C))+P(A)(1-P(B))P(C)+(1-P(A)P(B)P(C)=
解得,P(B)= ,P(C)=
,P(C)= 或P(B)=
或P(B)= ,P(C)=
,P(C)=
y= ,x=
,x= 或y=
或y= ,x=
,x= ;
;
(2)A、B、C均不发生的概率为P( )=(1-P(A))(1-P(B))(1-P(C))=
)=(1-P(A))(1-P(B))(1-P(C))=
点评:本体考查了相互独立事件同时发生的概率,应用乘法计算.
(2)用对立事件的概率分别求出A、B、C各自不发生的概率,再相乘即可.
解答:解:(1)设事件A发生的概率为P(A),事件B发生的概率为P(B),事件C发生的概率为P(C),
则P(A)=
 ,
,P(A
 )+P(
)+P( C)+P(
C)+P( )=P(A)(1-P(B))(1-P(C))+(1-P(A))(1-P(B))P(C)+(1-P(A))P(B)(1-P(C))=
)=P(A)(1-P(B))(1-P(C))+(1-P(A))(1-P(B))P(C)+(1-P(A))P(B)(1-P(C))= ,
,P(AB
 )+P(A
)+P(A C)+P(
C)+P( BC)=P(A)P(B)(1-P(C))+P(A)(1-P(B))P(C)+(1-P(A)P(B)P(C)=
BC)=P(A)P(B)(1-P(C))+P(A)(1-P(B))P(C)+(1-P(A)P(B)P(C)=
解得,P(B)=
 ,P(C)=
,P(C)= 或P(B)=
或P(B)= ,P(C)=
,P(C)=
y=
 ,x=
,x= 或y=
或y= ,x=
,x= ;
;(2)A、B、C均不发生的概率为P(
 )=(1-P(A))(1-P(B))(1-P(C))=
)=(1-P(A))(1-P(B))(1-P(C))=
点评:本体考查了相互独立事件同时发生的概率,应用乘法计算.

练习册系列答案
相关题目
 ,A、B、C中只有一个发生的概率为
,A、B、C中只有一个发生的概率为 ,A、B、C中只有一个不发生的概率是
,A、B、C中只有一个不发生的概率是 。
。