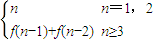Question

上一个n级台阶，若每步可上一级或两级，设上法总数为f（n），则下列猜想中正确的是（　　）

• A、f（n）=n
• B、f（n）=f（n-1）+f（n-2）
• C、f（n）=f（n-1）•f（n-2）
• D、f（n）=

  n n=1，2 f(n-1)+f(n-2) n≥3

Answer 1

分析：利用排列组合的知识，运用排除法排除不符合条件的选项，找出正确答案．

解答：解：由于n=1，B、C选项中f（n-1）=f（0），f（n-2）=f（-1）没实际意义，排除选项B，C
当有一级台阶，走法只有一种，即f（1）=1，
有两级台阶，有两种走法，即f（2）=2，同样f（3）=3，f（4）=5
由f（4）=5，A中f（4）=4≠5，排除选项A
故选D

点评：本题主要考查利用排列组合的知识解决数列的递推关系，利用排除法做选择题的方法．特殊值法、排除法这些常见的做选择题的方法要注意掌握．