题目内容
已知长方形ABCD的一组邻边长分别为3、4,沿对角线AC折成一个三棱锥,若记二面角B-AC-D的大小为θ( 0<θ<| π | 2 |
分析:根据已知中长方形ABCD的一组邻边长分别为3、4,沿对角线AC折成一个三棱锥,我们可以求出棱锥的外接球的半径,代入球的体积公式,即可得到答案.
解答:解:将长方形ABCD的一组邻边长分别为3、4,沿对角线AC折成一个三棱锥,
则三棱锥的外接球的球心落在AC的中点上
∵长方形ABCD的一组邻边长分别为3、4,
∴AC=5
则外接球的半径为
则该三棱锥的体积V=
故答案为:
则三棱锥的外接球的球心落在AC的中点上
∵长方形ABCD的一组邻边长分别为3、4,
∴AC=5
则外接球的半径为
| 5 |
| 2 |
则该三棱锥的体积V=
| 125π |
| 6 |
故答案为:
| 125π |
| 6 |
点评:本题考查的知识点是棱锥的几何特征,棱的体积公式,其中根据棱锥的几何特征,求出棱锥的外接球的半径,是解答本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,已知长方形ABCD的两条对角线的交点为E(1,0),且AB与BC所在的直线方程分别为:x+3y-5=0与ax-y+5=0.
如图,已知长方形ABCD的两条对角线的交点为E(1,0),且AB与BC所在的直线方程分别为:x+3y-5=0与ax-y+5=0.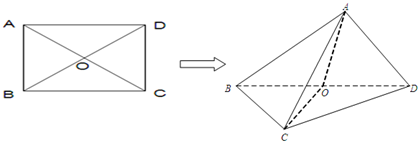

 ),则该三菱锥的外接球的体积为 .
),则该三菱锥的外接球的体积为 .