题目内容
设集合 =( )
=( )
A. | B. |
C. | D.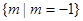 |
C
解析试题分析:因为集合根据一元二次不等式的解集和一元二次函数的性质知道,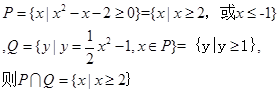
那么可知答案选C.
考点:本题主要考查了集合的交集的运算问题。
点评:解决该试题的关键是利用一元二次不等式的解集来得到集合P,Q同时结合交集的概念得到结论。

练习册系列答案
相关题目
设 是两个非空集合,定义
是两个非空集合,定义 与
与 的差集为:
的差集为: ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
下列各组对象能构成集合的有( )
(1)所有的正方体 (2)温州市区内的所有大超市
(3)所有的数学难题 (4)出名的舞蹈家
(5)某工厂2012年生产的所有产品 (6)直角坐标平面坐标轴上所有的点
| A.(1)(3) (5) | B.(1)(2)(4) |
| C.(1)(5)(6) | D.(2)(4)(6) |
设全集 ,集合
,集合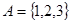 ,
,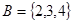 ,则
,则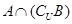 = ( )
= ( )
A.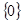 | B.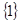 | C.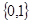 | D.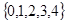 |
设集合 ,
,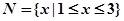 ,则
,则 ( )
( )
A. | B. | C. | D. |
设集合 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
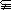 C D.A=B=C
C D.A=B=C

 ,则阴影部分表示的集合为( )
,则阴影部分表示的集合为( )



