题目内容
在-20与28之间插入3个数a、b、c，使它们5个数成等差数列，则插入的3个数a、b、c依次为
-8，4，16
-8，4，16
．分析：利用等差数列的通项公式即可得出．
解答：解：设此等差数列的公差为d，则28=-20+4d，解得d=12．
∴an=-20+12（n-1）=12n-32．
∴a=a2=12×2-32=-8，
b=a3=12×3-32=4，
c=a4=12×4-32=16．
因此插入的3个数a、b、c依次为-8，4，16．
故答案为-8，4，16．
∴an=-20+12（n-1）=12n-32．
∴a=a2=12×2-32=-8，
b=a3=12×3-32=4，
c=a4=12×4-32=16．
因此插入的3个数a、b、c依次为-8，4，16．
故答案为-8，4，16．
点评：本题考查了等差数列的通项公式，属于基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
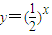的图象上，且数列{an} 是a1=1，公差为d的等差数列．
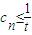（t∈R，t≠0）对一切正整数n恒成立；
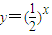的图象上，且数列{an} 是a1=1，公差为d的等差数列．
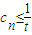（t∈R，t≠0）对一切正整数n恒成立；