题目内容
设向量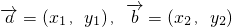 ,则
,则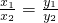 是
是 的________.
的________.
充分不必要
分析:利用向量的平行推导向量坐标之间的关系,通过已知关系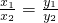 ,推导向量是否平行,然后判断充要条件即可.
,推导向量是否平行,然后判断充要条件即可.
解答:因为向量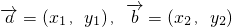 ,则
,则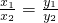 ,
,
即x1y2=x2y1,所以 ,
,
如果 ,可得x1y2=x2y1,推不出
,可得x1y2=x2y1,推不出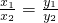 ,
,
所以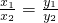 是
是 的充分不必要条件.
的充分不必要条件.
故答案为:充分不必要.
点评:判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:利用向量的平行推导向量坐标之间的关系,通过已知关系
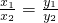 ,推导向量是否平行,然后判断充要条件即可.
,推导向量是否平行,然后判断充要条件即可.解答:因为向量
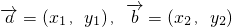 ,则
,则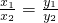 ,
,即x1y2=x2y1,所以
 ,
,如果
 ,可得x1y2=x2y1,推不出
,可得x1y2=x2y1,推不出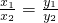 ,
,所以
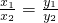 是
是 的充分不必要条件.
的充分不必要条件.故答案为:充分不必要.
点评:判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 为向量。则
为向量。则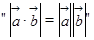 是
是 的( )
的( ) 为向量。则
为向量。则 是
是 的( )
的( ) ,则
,则 是
是 的( ).
的( ).