题目内容
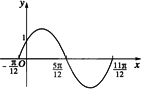
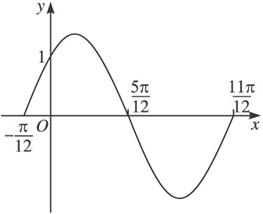
函数f1(x)=Asin(ωx+φ)(A＞0,ω＞0,|φ|＜
)的一段图象过点(0,1),如图1-6-10所示.(1)求函数f1(x)的表达式;
(2)将函数y=f1(x)的图象向右平移
个单位,得函数y=f2(x)的图象,求y=f2(x)的最大值,并求出此时自变量x的集合.
图1-6-10
解:(1)由图知,T=π,于是ω=
=2.
将y=Asin2x的图象向左平移,
得y=Asin(2x+φ)的图象.
于是φ=2·=
.
将(0,1)代入y=Asin(2x+
),得A=2.
故f1(x)=2sin(2x+
).
(2)依题意,f2(x)=2sin［2(x-
)+ 
］
=-2cos(2x+
),
当2x+
=2kπ+π,
即x=kπ+
(k∈Z)时,ymax=2.
x的取值集合为{x|x=kπ+
,k∈Z }.
练习册系列答案
相关题目
)的一段图象过点(0，1)，如图所示．
个单位，得函数y＝f2(x)的图象，求y＝f2(x)的最大值，并求出此时自变量x的集合．
)的一段图象过点（0，1），如下图所示.
个单位，得函数y=f2(x)的图象，求y=f2(x)的最大值,并求出此时自变量x的集合.