Question

5名工人独立地工作，假定每名工人在1小时内平均12分钟需要电力（即任一时刻需要电力的概率为12/60）

（1）设X为某一时刻需要电力的工人数，求 X的分布列及期望；

（2）如果同一时刻最多能提供3名工人需要的电力，求电力超负荷的概率，并解释实际意义．

 

Answer 1

【答案】

（1）EX＝1；（2）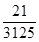

【解析】本试题主要考查了二项分布的运用。

（1）因为5名工人独立地工作，假定每名工人在1小时内平均12分钟需要电力（即任一时刻需要电力的概率为12/60），那么可以看作5此独立重复试验，那么利用概率公式解得。

（2）同时利用设电力超负荷的事件为A，则

P（A）＝P（X≥4）＝××＋＝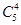

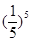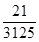
得到结论。

解：（1）X可能取的值为0，1，2，3，4，5，且X~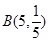

即P（X＝i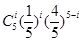）＝（i＝0，1，2，3，4，5），∴EX＝5×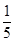＝1

（2）设电力超负荷的事件为A，则

P（A）＝P（X≥4）＝××＋＝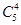

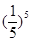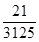
因P（A）的值不足1％，即发生超负荷的可能性非常小，不影响正常工作