Question

设l₁，l₂是两条直线，α，β是两个平面，A为一点，下列命题中正确的命题是     ．
①若l₁?α，l₂∩α=A，则l₁与l₂必为异面直线；
②若α⊥β，l₁?α，则l₁⊥β；
③l₁?α，l₂?β，l₁∥β，l₂∥α，则α∥β；
④若l₁∥α，l₂∥l₁，则l₂∥α或l₂?α．

Answer 1

【答案】分析：对①②③均可找到其反例，所以①②③错，而④，可以借助于画草图来说明其成立．
解答：解：①错，两直线可相交于点A；
②错，不符合面面垂直的性质定理的条件；
③错，不符合面面平行的判定定理条件；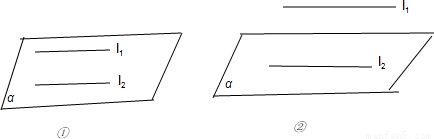
④正确，空间想象即可．
故答案为：④
点评：本题是对直线和平面位置关系的综合考查，空间中，直线和平面的位置关系有三种，平行，相交，在平面内．