题目内容
若△ABC边长为a,b,c,且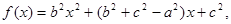 则f(x)的图象( )
则f(x)的图象( )
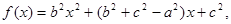 则f(x)的图象( )
则f(x)的图象( )| A.在x轴的上方 | B.在x轴的下方 | C.与x轴相切 | D.与x轴交于两点 |
A
Δ=(b²+c²-a²)²-4b²c²
=(b²+c²-a²+2bc)(b²+c²-a²-2bc)
=[(b+c)²-a²][(b-c)²-a²]
=(b+c+a)(b+c-a)(b-c+a)(b-c-a)
∵a、b、c为三角形ABC的三边,
∴(b+c+a)>0,(b+c-a)>0,(b-c+a)>0,(b-c-a)<0,
∴Δ<0,
∴f(x)的图象与X轴没有交点。
又∵二次项系数为b2>0,
∴抛物线开口向上,且与X轴没有交点,
∴图象在X轴上方。故选A。

练习册系列答案
相关题目
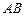 至少长2.8m,
至少长2.8m,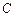 为
为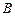 到
到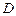 的距离比
的距离比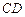 的长小0.5m,
的长小0.5m,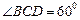 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?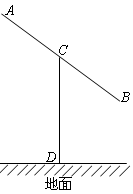
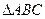 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为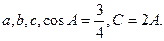
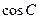 的值;
的值;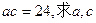 的值。
的值。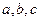 分别为
分别为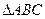 的内角
的内角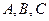 的对边,
的对边,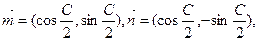
 与
与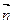 的夹角为
的夹角为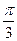
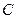 的大小;
的大小;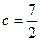 ,
, ,求
,求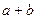 的值。
的值。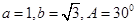 ,则
,则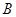 等于
等于  中,AB=3,AC=2,BC=
中,AB=3,AC=2,BC=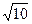 ,则
,则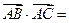 ( )
( )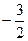
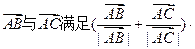
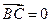
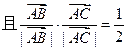 ,则△ABC为 ( )
,则△ABC为 ( ) 上,则这个正三角形的边长为___________.
上,则这个正三角形的边长为___________.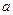 、
、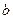 、
、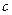 分别是
分别是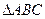 的三个内角
的三个内角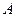 、
、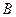 、
、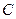 所对的边,
所对的边,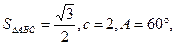 求
求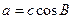 ,且
,且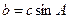 ,试判断
,试判断