题目内容
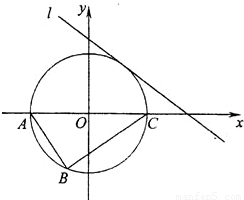 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-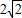 ),顶点C在x轴上.
),顶点C在x轴上.(1)求BC边所在直线方程;
(2)M为Rt△ABC外接圆的圆心,求圆M的方程;
(3)直线l与圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程.
【答案】分析:(1)由顶点B,C的坐标可求BC的斜率,再根据点C(3,0)可求BC边所在直线方程;
(2)Rt△ABC外接圆是以O为原点,3为半径的圆,从而可求圆M的方程;
(3)设直线方程为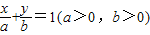 ,利用直线l与圆相切可知
,利用直线l与圆相切可知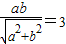 ,从而利用均值不等式有ab≥18,因此可求直线方程.
,从而利用均值不等式有ab≥18,因此可求直线方程.
解答:解:(1)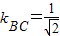 ,∵C(3,0),∴
,∵C(3,0),∴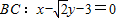 .
.
(2)由(1)知C(3,0),∵M为Rt△ABC外接圆的圆心,所以M坐标为(0,0),所以圆M:x2+y2=9.
(3)设直线方程为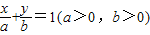 ,即
,即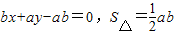 .
.
由相切可知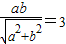 .由均值不等式
.由均值不等式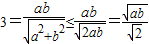 ,则ab≥18.
,则ab≥18.
所以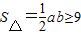 ,当且仅当
,当且仅当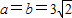 时等号成立,则直线方程为
时等号成立,则直线方程为 .
.
点评:本题主要考查直线与圆的方程的求解,考查基本不等式的运用,属于基础题
(2)Rt△ABC外接圆是以O为原点,3为半径的圆,从而可求圆M的方程;
(3)设直线方程为
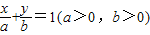 ,利用直线l与圆相切可知
,利用直线l与圆相切可知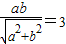 ,从而利用均值不等式有ab≥18,因此可求直线方程.
,从而利用均值不等式有ab≥18,因此可求直线方程.解答:解:(1)
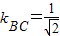 ,∵C(3,0),∴
,∵C(3,0),∴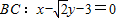 .
.(2)由(1)知C(3,0),∵M为Rt△ABC外接圆的圆心,所以M坐标为(0,0),所以圆M:x2+y2=9.
(3)设直线方程为
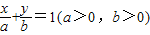 ,即
,即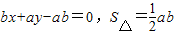 .
.由相切可知
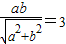 .由均值不等式
.由均值不等式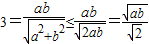 ,则ab≥18.
,则ab≥18.所以
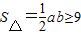 ,当且仅当
,当且仅当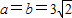 时等号成立,则直线方程为
时等号成立,则直线方程为 .
.点评:本题主要考查直线与圆的方程的求解,考查基本不等式的运用,属于基础题

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,- 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,- ),顶点C在x轴上.
),顶点C在x轴上.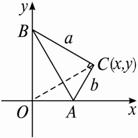
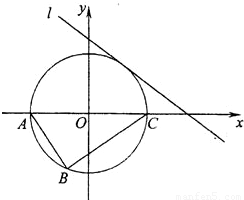 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-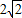 ),顶点C在x轴上.
),顶点C在x轴上.