题目内容
已知几何体A-BCED的三视图、直观图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体A-BCED的体积V的大小;
(2)求二面角A-ED-B的余弦值.
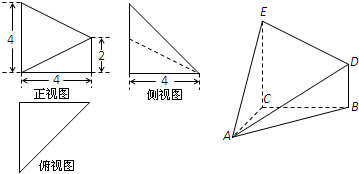
(1)求此几何体A-BCED的体积V的大小;
(2)求二面角A-ED-B的余弦值.

分析:(1)由三视图可知,AC=BC=CE=4,BD=2,且AC、BC、CE两两互相垂直.代入棱锥体积公式,可得答案.
(2)过C作CG⊥DE交DE于G,连AG.可得∠AGC为二面角A-ED-B的平面角,解△ACG可得答案
(2)坐标法:分别求出平面BDE的一个法向量和平面ADE的一个法向量,代入向量夹角公式,可得二面角A-ED-B的余弦值.
(2)过C作CG⊥DE交DE于G,连AG.可得∠AGC为二面角A-ED-B的平面角,解△ACG可得答案
(2)坐标法:分别求出平面BDE的一个法向量和平面ADE的一个法向量,代入向量夹角公式,可得二面角A-ED-B的余弦值.
解答:解:(1)由三视图可知,AC=BC=CE=4,BD=2,
且AC、BC、CE两两互相垂直.
∴几何体A-BCED的体积
V=
•SBCED•AC=16(6分)
(2)AC⊥平面BCE,
过C作CG⊥DE交DE于G,连AG.
可得DE⊥平面ACG,从而AG⊥DE
∴∠AGC为二面角A-ED-B的平面角. (10分)
在△ACG中,∠ACG=90°,AC=4,CG=
,
∴AG=
=
.
∴cos∠AGC=
=
.
∴二面角A-ED-B的余弦值为
. (14分)
方法二:(坐标法)
(2)平面BDE的一个法向量为
=(4,0,0),(8分)
设平面ADE的一个法向量为
=(x,y,z),
⊥
,
⊥
,
∵
=(-4,4,2),
=(0,-4,2),
∴
•
=0,
•
=0
从而-4x+4y+2z=0,-4y+2z=0,
令y=1,则
=(2,1,2),(12分)
显然二面角A-ED-B是锐二面角,设其平面角为θ,
则cosθ=|cos<
,
>|=
∴二面角A-ED-B的余弦值为
.(14分)
且AC、BC、CE两两互相垂直.
∴几何体A-BCED的体积
V=
| 1 |
| 3 |
(2)AC⊥平面BCE,
过C作CG⊥DE交DE于G,连AG.
可得DE⊥平面ACG,从而AG⊥DE
∴∠AGC为二面角A-ED-B的平面角. (10分)
在△ACG中,∠ACG=90°,AC=4,CG=
8
| ||
| 5 |
∴AG=
42+(
|
| 12 |
| 5 |
| 5 |
∴cos∠AGC=
| CG |
| AG |
| 2 |
| 3 |
∴二面角A-ED-B的余弦值为
| 2 |
| 3 |
方法二:(坐标法)
(2)平面BDE的一个法向量为
| CA |
设平面ADE的一个法向量为
| n |
| n |
| AD |
| n |
| DE |
∵
| AD |
| DE |
∴
| n |
| AD |
| n |
| DE |
从而-4x+4y+2z=0,-4y+2z=0,
令y=1,则
| n |
显然二面角A-ED-B是锐二面角,设其平面角为θ,
则cosθ=|cos<
| CA |
| n |
| 2 |
| 3 |
∴二面角A-ED-B的余弦值为
| 2 |
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,棱锥的体积公式,根据三视图判断出几何体的形状及棱长是解答(1)的关键,(2)中求二面角思路有几何法:求出二面角的平面角,将求空间角转化为解三角形问题,向量法:构造空间直角坐标系,将二面角问题转化为法向量夹角问题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
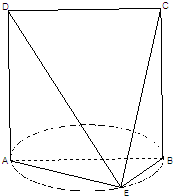 如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.
如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE. 如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.
如图,已知四边形ABCD是边长为4cm的正方形,直线AD垂直于以AB为直径的圆所在的平面,点E是该圆上异于A,B的一点,连接AE、BE、DE、CE.