题目内容
已知二面角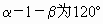
，A∈l，C∈l，AB=AC=CD=1，
，
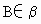，且AB⊥l，CD⊥l，求DB的长及异面直线l与DB的距离．
答案：
解析：
解析：
|
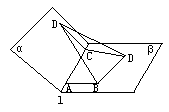
解：如图，作EC⊥l，使CE＝1，则
∴ ∠DEB＝ 连DE，在△DCE中，CE＝CD＝1，
在Rt△DEB中， 所以DB=2． ②如图，AC⊥平面DCE中，AC与DE异面， 在平面DCE中，作CF⊥DE于E．
∴ CF是异面直线AC与DE的公垂线． ∴ △DCE是等腰三角形． ∴ CF⊥DE，同时CF是∠DCE的平分线．
∴ AC∥BE，即AC∥平面BDE． CF是直线AC与平面BDE的距离．
∴ CF是异面直线AC与DB的距离为
|
．
．
．
练习册系列答案
相关题目
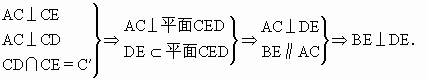
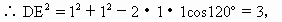
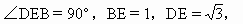
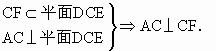
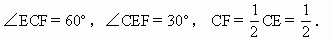
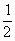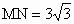，M到棱的距离MP＝6，则N点到a
距离是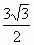
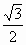
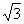
，则P点在9上的射影
到平面a
的距离为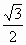
，M到棱的距离MP＝6，则N点到a
距离是
，则P点在β上的射影
到平面a
的距离为
