题目内容
已知函数f(x)bx3+ax2-3x
(1)若f(x)在x=1和x=3处取得极值,求a,b的值;
(2)若f(x)为实数集R上的单调函数,且b≥-1,设点P的坐标为(a,b),试求出点P的轨迹所形成的图形的面积S.
(1)若f(x)在x=1和x=3处取得极值,求a,b的值;
(2)若f(x)为实数集R上的单调函数,且b≥-1,设点P的坐标为(a,b),试求出点P的轨迹所形成的图形的面积S.
分析:(1)先求出函数的导函数,然后利用f(x)在x=1和x=3处取得极值是导函数方程的两个根,建立方程组,解之即可;
(2)根据函数的单调性转化成f′(x)≥0恒成立或者f′(x)≤0恒成立,然后建立关系式,最后利用定积分表示出所围成图形的面积即可.
(2)根据函数的单调性转化成f′(x)≥0恒成立或者f′(x)≤0恒成立,然后建立关系式,最后利用定积分表示出所围成图形的面积即可.
解答:解:(1)f(x)=bx3+ax2-3x,f′(x)=3bx2+2ax-3
∵f(x)在x=1和x=3处取得极值
∴x=1和x=3是f′(x)=3bx2+2ax-3=0的两个根
代入方程解之得a=2,b=-
(2)当b=0时,由f(x)在R上单调知a=0
当b≠0时,由f(x)在R上单调⇒f′(x)≥0恒成立或者f′(x)≤0恒成立
f′(x)=3bx2+2ax-3∴△=4a2+36b≤0可得b≤-
a2
∴面积S=
(1-
x2)dx=4
∵f(x)在x=1和x=3处取得极值
∴x=1和x=3是f′(x)=3bx2+2ax-3=0的两个根
代入方程解之得a=2,b=-
| 1 |
| 3 |
(2)当b=0时,由f(x)在R上单调知a=0
当b≠0时,由f(x)在R上单调⇒f′(x)≥0恒成立或者f′(x)≤0恒成立
f′(x)=3bx2+2ax-3∴△=4a2+36b≤0可得b≤-
| 1 |
| 9 |
∴面积S=
| ∫ | 3 -3 |
| 1 |
| 9 |
点评:本题主要考查了利用导数研究函数的极值以及单调性,同时考查了利用定积分求围成图形的面积,考查的知识点较多,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,且b<0,试判断函数F(x)的单调性;
,且b<0,试判断函数F(x)的单调性;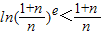 恒成立.
恒成立.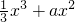 +bx+c在x=1及x=3时取到极值.
+bx+c在x=1及x=3时取到极值.