题目内容
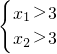 是
是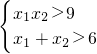 成立的
成立的
- A.充分而不必要条件
- B.必要而不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析:分充分性和必要性两方面加以论证:根据不等式的性质,可证明出充分性成立;再通过举出反例说明必要性是不成立的.因此得出正确选项.
解答:①充分性,当x1>3且x2>3时,
根据不等式的性质可得:x1x2>9且x1+x2>6
∴充分性成立
②必要性,当x1x2>9且x1+x2>6成立,x1>3且x2>3不一定成立‘
比如:x1=2,x2=8满足“x1x2>9且x1+x2>6”,但“x1>3且x2>3”不成立
∴必要性不成立
所以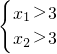 是
是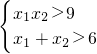 成立的充分不必要条件
成立的充分不必要条件
故选A
点评:本题着重考查了必要条件、充分条件与充要条件判断的知识点,属于基础题.解题时应注意要证明命题成立必须有严格的推理过程,但要说明某命题不正确,只要举一反例即可.
分析:分充分性和必要性两方面加以论证:根据不等式的性质,可证明出充分性成立;再通过举出反例说明必要性是不成立的.因此得出正确选项.
解答:①充分性,当x1>3且x2>3时,
根据不等式的性质可得:x1x2>9且x1+x2>6
∴充分性成立
②必要性,当x1x2>9且x1+x2>6成立,x1>3且x2>3不一定成立‘
比如:x1=2,x2=8满足“x1x2>9且x1+x2>6”,但“x1>3且x2>3”不成立
∴必要性不成立
所以
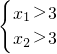 是
是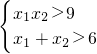 成立的充分不必要条件
成立的充分不必要条件故选A
点评:本题着重考查了必要条件、充分条件与充要条件判断的知识点,属于基础题.解题时应注意要证明命题成立必须有严格的推理过程,但要说明某命题不正确,只要举一反例即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是“
是“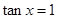 ”成立的
”成立的