题目内容
(12分)设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若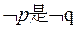 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.
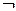
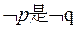 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.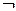
实数a的取值范围是[0,].
解:设A={x|(4x-3)2≤1},
B={x|x2-(2a+1)x+a(a+1)≤0},
易知A={x|≤x≤1},
B={x|a≤x≤a+1}.
 由 p是 q的必要不充分条件,从而p是q的充分不必要条件,
由 p是 q的必要不充分条件,从而p是q的充分不必要条件,
即A ?B,
?B,
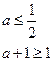 且两等号不能同时取。
且两等号不能同时取。
故所求实数a的取值范围是[0,].
B={x|x2-(2a+1)x+a(a+1)≤0},
易知A={x|≤x≤1},
B={x|a≤x≤a+1}.
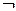
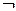
 由 p是 q的必要不充分条件,从而p是q的充分不必要条件,
由 p是 q的必要不充分条件,从而p是q的充分不必要条件,即A
 ?B,
?B, 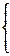
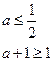 且两等号不能同时取。
且两等号不能同时取。故所求实数a的取值范围是[0,].

练习册系列答案
相关题目
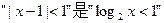 的 ( )
的 ( )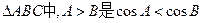 的 ( )
的 ( )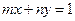 同时经过第一、三、四象限的必要不充分条件
同时经过第一、三、四象限的必要不充分条件 是(
是(  )
)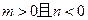
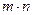 <0
<0 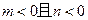

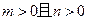
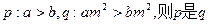 的 ( )
的 ( )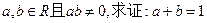 成立的充要条件是
成立的充要条件是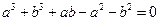 。
。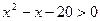 ,q:
,q: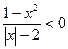 ,则p是q的 ( )
,则p是q的 ( )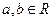 ,则“
,则“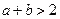 且
且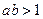 ”是“
”是“ 且
且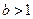 ”的 条件
”的 条件