题目内容
(1)已知|z1|=|z2|=|z1-z2|=1,求|z1+z2|的值;(2)设复数z满足|z|=1,且(3+4i)•z是纯虚数,求
. | z |
分析:(1)根据要求复数的和的模长,对所求的结果平方,根据平方后|z1|与|z2|与|z1-z2|与|z1+z2|四者之间的关系,把要求的结果,变化为已知条件,求出结果.
(2)设出z复数的式子,根据两个复数的乘积是一个纯虚数,得到a和b之间的关系,根据模长是1,又得到一个关系,根据列出的方程组求a和b的值,得到复数z,写出共轭复数.
(2)设出z复数的式子,根据两个复数的乘积是一个纯虚数,得到a和b之间的关系,根据模长是1,又得到一个关系,根据列出的方程组求a和b的值,得到复数z,写出共轭复数.
解答:解:(1)|z1+z2|2=2(|z1|2+|z2|2)-|z1-z2|2=3,|z1+z2|=
(2)设z=a+bi,(3+4i)•z=(3+4i)(a+bi)=3a-4b+(4a+3b)i是纯虚数,
则3a-4b=0
?
,或
,
=
-
i,或-
+
i
| 3 |
(2)设z=a+bi,(3+4i)•z=(3+4i)(a+bi)=3a-4b+(4a+3b)i是纯虚数,
则3a-4b=0
|
|
|
. |
| z |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
点评:本题考查复数的模长的运算,考查共轭复数,考查复数的代数形式的乘法运算,是一个综合题,本题第一问所用的方法比较灵活.

练习册系列答案
相关题目
 。
。 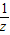 =
=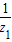 +
+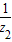 ,求z.
,求z.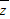 =4+3i,求z及
=4+3i,求z及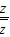 .
.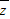 .
.