题目内容
设Sn为数列{an}为前n项和,对任意的 都有
都有 (m为常数且m>0)
(m为常数且m>0)
(1)求证:{an}为等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足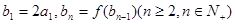 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)在(2)的条件下,求数列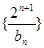 的前n项和Tn。
的前n项和Tn。
【答案】
(1)证明 为等比数列;(2)
为等比数列;(2)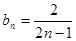 ;
;
(3)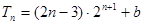
【解析】
试题分析:由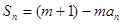 ①
①
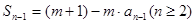 ②
②
①-②得:
 即
即 为等差数列
为等差数列
(2)n=1时,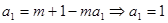
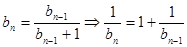 即
即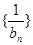 为d=1的等比数列
为d=1的等比数列
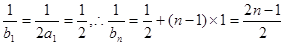
即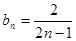
(3)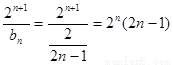 用错位相减法得
用错位相减法得
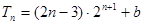
考点:本题主要考查等差数列、等比数列的的基础知识,“错位相消法”求和。
点评:中档题,本题具有较强的综合性,本解答从确定通项公式入手,认识到数列的特征,利用“错位相消法”达到求和目的。“分组求和法”“裂项相消法”“错位相减法”是高考常常考到数列求和方法。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目