题目内容
15.在等差数列{an}中,(1)a6=10,S5=5,求a8;
(2)a2+a4=$\frac{48}{5}$,求S5.
分析 (1)由题意可得首项a1和公差d的方程组,解方程组由通项公式可得a8的值;
(2)由条件和等差数列的性质可得a1+a5=$\frac{48}{5}$,代入求和公式计算可得S5
解答 解:(1)设等差数列{an}的公差为d,
∵a6=10,S5=5,∴a1+5d=10,5a1+$\frac{5×4}{2}$d=5,
解得a1=-5,d=3
∴a8=-5+7×3=16;
(2)∵等差数列{an}中a2+a4=$\frac{48}{5}$,
∴由等差数列的性质可得a1+a5=$\frac{48}{5}$,
∴S5=$\frac{5({a}_{1}+{a}_{5})}{2}$=$\frac{5×\frac{48}{5}}{2}$=24.
点评 本题考查等差数列的通项公式和性质,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.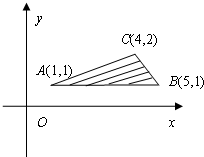 在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )
在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )
 在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )
在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )| A. | $\frac{2}{7}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
20.《莱茵德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题:把100个面包分给5个人,使每个人的所得成等差数列,且使较大的三份之和的$\frac{1}{7}$是较小的两份之和,则最小一份的量为( )
| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{6}$ |
4. 执行如图所示的程序框图,输出的s的值为( )
执行如图所示的程序框图,输出的s的值为( )
 执行如图所示的程序框图,输出的s的值为( )
执行如图所示的程序框图,输出的s的值为( )| A. | $\frac{9}{5}$ | B. | $\frac{7}{4}$ | C. | $\frac{11}{6}$ | D. | $\frac{4}{5}$ |
5.已知点F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两焦点,若双曲线左支上存在点P与点F2关于直线y=$\frac{b}{a}$x对称,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
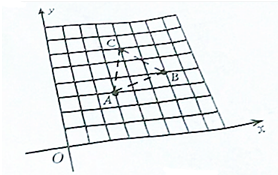 如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).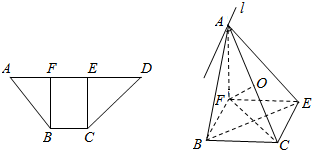 如图,梯形ABCD中,CE⊥AD于E,BF⊥AD于F,且AF=BF=BC=1,$DE=\sqrt{2}$,现将△ABF,△CDE分别沿BF与CE翻折,使点A与点D重合,点O为AC的中点,设面ABF与面CDE相交于直线l,
如图,梯形ABCD中,CE⊥AD于E,BF⊥AD于F,且AF=BF=BC=1,$DE=\sqrt{2}$,现将△ABF,△CDE分别沿BF与CE翻折,使点A与点D重合,点O为AC的中点,设面ABF与面CDE相交于直线l,