题目内容
(5分)(2011•重庆)若函数f(x)=x+ (x>2),在x=a处取最小值,则a=( )
(x>2),在x=a处取最小值,则a=( )
A.1+ | B.1+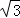 | C.3 | D.4 |
C
解析试题分析:把函数解析式整理成基本不等式的形式,求得函数的最小值和此时x的取值.
解:f(x)=x+ =x﹣2+
=x﹣2+ +2≥4
+2≥4
当x﹣2=1时,即x=3时等号成立.
∵x=a处取最小值,
∴a=3
故选C
点评:本题主要考查了基本不等式的应用.考查了分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若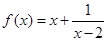
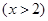 在
在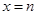 处取得最小值,则
处取得最小值,则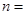 ( )
( )
A.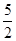 | B.3 | C.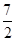 | D.4 |
若一元二次不等式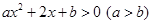 的解集为
的解集为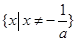 ,则
,则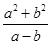 的最小值是( )
的最小值是( )
A.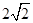 | B. | C.2 | D.1 |
若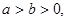 则下列不等式成立的是 ( )
则下列不等式成立的是 ( )
A. | B.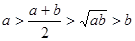 |
C.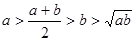 | D.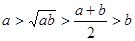 |
已知 ,且
,且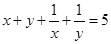 ,则
,则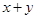 的最大值是( )
的最大值是( )
| A.3 | B.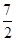 | C.4 | D.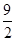 |
(2013·西安模拟)已知x>0,y>0,lg2x+lg8y=lg2,则 +
+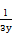 的最小值是( )
的最小值是( )
| A.2 | B.2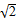 | C.4 | D.2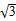 |
若x≥0,y≥0且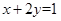 ,那么2x+3y2的最小值为( )
,那么2x+3y2的最小值为( )
| A.2 |
B.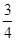 |
C.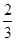 |
| D.0 |
已知a>0,b>0,a+b=2,则 +
+ 的最小值是( )
的最小值是( )
A. | B.4 | C. | D.5 |