题目内容
已知两个数列{Sn}、{Tn}分别:当n∈N*,Sn=1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
(1)求S1,S2,T1,T2;
(2)猜想Sn与Tn的关系,并用数学归纳法证明.
分析:(1)由已知直接利用n=1,2,求出S1,S2,T1,T2的值;
(2)利用(1)的结果,直接猜想Sn=Tn,然后利用数学归纳法证明,①验证n=1时猜想成立;②假设n=k时,Sk=Tk,通过假设证明n=k+1时猜想也成立即可.
(2)利用(1)的结果,直接猜想Sn=Tn,然后利用数学归纳法证明,①验证n=1时猜想成立;②假设n=k时,Sk=Tk,通过假设证明n=k+1时猜想也成立即可.
解答:解:(1)S1=1-
=
,S2=1-
+
-
=
T1=
=
,T2=
+
=
(2分)
(2)猜想:Sn=Tn(n∈N*),即:
1-
+
-
+…+
-
=
+
+
+…+
.
(n∈N*)(5分)
下面用数学归纳法证明:
①当n=1时,已证S1=T1(6分)
②假设n=k时,Sk=Tk(k≥1,k∈N*),
即:1-
+
-
+…+
-
=
+
+
+…+
(8分)
则:Sk+1=Sk+
-
=Tk+
-
(10分)
=
+
+
+…+
+
-
(11分)
=
+
+…+
+(
-
)
=
+
+…+
+
=Tk+1,
由①,②可知,对任意n∈N*,Sn=Tn都成立.(14分)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
T1=
| 1 |
| 1+1 |
| 1 |
| 2 |
| 1 |
| 2+1 |
| 1 |
| 2+2 |
| 7 |
| 12 |
(2)猜想:Sn=Tn(n∈N*),即:
1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
(n∈N*)(5分)
下面用数学归纳法证明:
①当n=1时,已证S1=T1(6分)
②假设n=k时,Sk=Tk(k≥1,k∈N*),
即:1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
则:Sk+1=Sk+
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
=
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
=
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k+1 |
| 1 |
| k+1 |
| 1 |
| 2(k+1) |
=
| 1 |
| (k+1)+1 |
| 1 |
| (k+1)+2 |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
由①,②可知,对任意n∈N*,Sn=Tn都成立.(14分)
点评:本题是中档题,考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.

练习册系列答案
相关题目
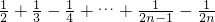 ,Tn=
,Tn=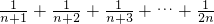 .
.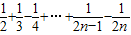 ,Tn=
,Tn=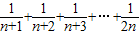 .
.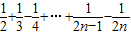 ,Tn=
,Tn=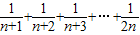 .
.