题目内容
已知k<1,求不等式| k(x-1) | x-2 |
分析:分两种情况考虑:当x-2大于0时,在不等式两边都乘以x-2,不等号方向不变去掉分母后,由k小于0得到k-1小于0,即可求出原不等式的解集;当x-2小于0时,在不等式两边都乘以x-2,不等号方向改变去掉分母后,同理由k-1小于0,即可求出原不等式的解集,综上,得到原不等式的解集.
解答:解:当x-2>0即x>2时,原不等式去分母得:kx-k>x-2,
即(k-1)x>k-2,又k<1,即k-1<0,
解得:x<
=1+
<1,则原不等式无解;
当x-2<0即x<2时,原不等式去分母得:kx-k<x-2,
即(k-1)x<k-2,又k<1,即k-1<0,
解得:x>
,原不等式的解集为:
<x<2,
综上,原不等式的解集为(
,2).
即(k-1)x>k-2,又k<1,即k-1<0,
解得:x<
| k-2 |
| k-1 |
| 1 |
| k-1 |
当x-2<0即x<2时,原不等式去分母得:kx-k<x-2,
即(k-1)x<k-2,又k<1,即k-1<0,
解得:x>
| k-2 |
| k-1 |
| k-2 |
| k-1 |
综上,原不等式的解集为(
| k-2 |
| k-1 |
点评:此题考查了其他不等式的解法,考查了分类讨论的数学思想,是一道基础题;学生在去分母时注意考虑x-2的正负决定不等号改变与否.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
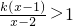 的解集.
的解集.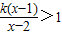 的解集.
的解集.