��Ŀ����
ͳ���г������ϵ����һ��������������x��y֮��������ع�ϵ��ǿ��������㹫ʽ��r=
���У�x1��y1������x2��y2����������xn��yn����ɢ��ͼ�е������㣬
=
xi��
=
yi��֤����r=
��
| ||||||||||||
|
. |
| x |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| y |
| 1 |
| n |
| n |
 |
| i=1 |
| ||||||||||||
|
������������ȫƽ����ʽ��ƽ�����ļ��㹫ʽ�ֱ�ѷ��ӷ�ĸչ�����㼴��֤����
���֤������
(xi-
)2=(
-2x1
+
2)+��+(
-2xn
+
2)
=(
+
+��+
)-2
(x1+x2+��+xn)+n
2
=
-2n
2+n
2=
-n
2��
ͬ��
(yi-
)2=
-n
2��
��
(xi-
)(yi-
)=(x1-
)(y1-
)+��+(xn-
)(yn-
)
=(x1y1-x1
-y1
)+(x2y2-x2
-y2
)+��+(xnyn-xn
-yn
)+n
=
xiyi-n
-n
+n
=
xiyi-n
��
��r=
��
| n |
 |
| i=1 |
. |
| x |
| x | 2 1 |
. |
| x |
. |
| x |
| x | 2 n |
. |
| x |
. |
| x |
=(
| x | 2 1 |
| x | 2 2 |
| x | 2 n |
. |
| x |
. |
| x |
=
| n |
 |
| i=1 |
| x | 2 i |
. |
| x |
. |
| x |
| n |
 |
| i=1 |
| x | 2 i |
. |
| x |
ͬ��
| n |
 |
| i=1 |
. |
| y |
| n |
 |
| i=1 |
| y | 2 i |
. |
| y |
��
| n |
 |
| i=1 |
. |
| x |
. |
| y |
. |
| x |
. |
| y |
. |
| x |
. |
| y |
=(x1y1-x1
. |
| y |
. |
| x |
. |
| y |
. |
| x |
. |
| y |
. |
| x |
. |
| x |
. |
| y |
=
| n |
 |
| i=1 |
. |
| x |
. |
| y |
. |
| x |
. |
| y |
. |
| x |
. |
| y |
| n |
 |
| i=1 |
. |
| x |
. |
| y |
��r=
| ||||||||||||||||
|
����������������ȫƽ����ʽ��ƽ�����ļ��㹫ʽ�ǽ���ʹ�ùؼ���

��ϰ��ϵ�д�
�����Ŀ

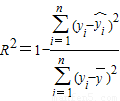 ��
��