题目内容
已知向量 =
= ,
, =
= (其中ω为正常数)
(其中ω为正常数)(Ⅰ)若
 ,求
,求 ∥
∥ 时tanx的值;
时tanx的值;(Ⅱ)设f(x)=
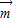 •
• -2,若函数f(x)的图象的相邻两个对称中心的距离为
-2,若函数f(x)的图象的相邻两个对称中心的距离为 ,求f(x)在区间
,求f(x)在区间 上的最小值.
上的最小值.
【答案】分析:(Ⅰ)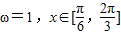 ,利用
,利用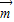 ∥
∥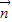 ,推出
,推出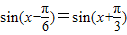 ,然后利用两角差与和的正弦函数,化简求出tanx的值;
,然后利用两角差与和的正弦函数,化简求出tanx的值;
(Ⅱ)先求f(x)=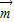 •
•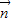 -2,根据函数f(x)的图象的相邻两个对称中心的距离为
-2,根据函数f(x)的图象的相邻两个对称中心的距离为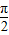 ,确定周期求出ω,然后求f(x)在区间
,确定周期求出ω,然后求f(x)在区间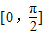 上的最小值.
上的最小值.
解答:解:(Ⅰ)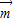 ∥
∥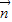 时,
时,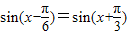 ,(2分)
,(2分)
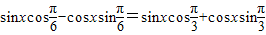
则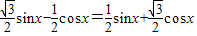 (4分)
(4分)
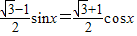 ,
,
所以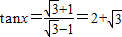 (6分)
(6分)
(Ⅱ)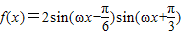 =
=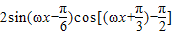 =
=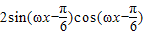 =
=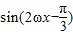 .(9分)
.(9分)
(或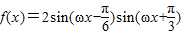 =
=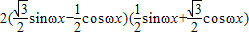 =
=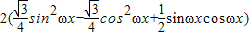 =
=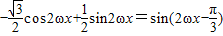 (9分)
(9分)
∵函数f(x)的图象的相邻两个对称中心的距离为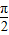
∴f(x)的最小正周期为π,又ω为正常数,
∴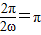 ,解之,得ω=1.(11分)
,解之,得ω=1.(11分)
故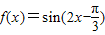 .
.
因为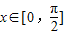 ,所以
,所以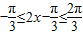 .
.
故当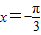 时,f(x)取最小值
时,f(x)取最小值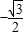 (14分)
(14分)
点评:本题考查函数y=Asin(ωx+φ)的图象变换,平行向量与共线向量,平面向量数量积的运算,考查计算能力,是基础题.
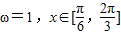 ,利用
,利用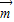 ∥
∥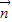 ,推出
,推出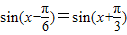 ,然后利用两角差与和的正弦函数,化简求出tanx的值;
,然后利用两角差与和的正弦函数,化简求出tanx的值;(Ⅱ)先求f(x)=
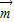 •
•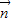 -2,根据函数f(x)的图象的相邻两个对称中心的距离为
-2,根据函数f(x)的图象的相邻两个对称中心的距离为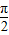 ,确定周期求出ω,然后求f(x)在区间
,确定周期求出ω,然后求f(x)在区间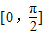 上的最小值.
上的最小值.解答:解:(Ⅰ)
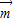 ∥
∥ 时,
时,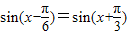 ,(2分)
,(2分)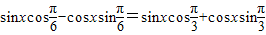
则
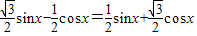 (4分)
(4分)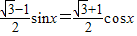 ,
,所以
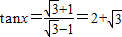 (6分)
(6分)(Ⅱ)
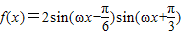 =
=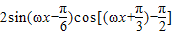 =
=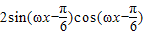 =
=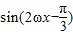 .(9分)
.(9分)(或
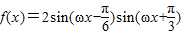 =
=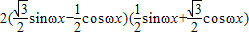 =
=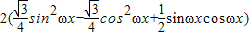 =
=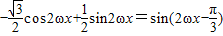 (9分)
(9分)∵函数f(x)的图象的相邻两个对称中心的距离为
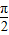
∴f(x)的最小正周期为π,又ω为正常数,
∴
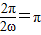 ,解之,得ω=1.(11分)
,解之,得ω=1.(11分)故
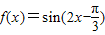 .
.因为
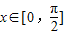 ,所以
,所以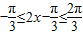 .
.故当
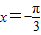 时,f(x)取最小值
时,f(x)取最小值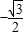 (14分)
(14分)点评:本题考查函数y=Asin(ωx+φ)的图象变换,平行向量与共线向量,平面向量数量积的运算,考查计算能力,是基础题.

练习册系列答案
相关题目
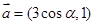 ,
, ,且
,且 ,其中
,其中 .
.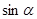 和
和 的值;
的值; ,
, ,求角
,求角 的值.
的值.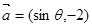 与
与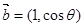 互相垂直,其中
互相垂直,其中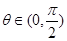 .
.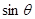 和
和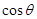 的值;
的值;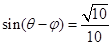 ,
, ,求
,求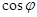 的值.
的值.