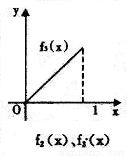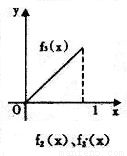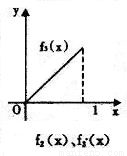题目内容
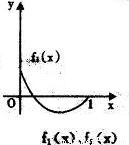
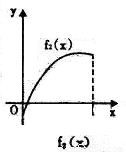
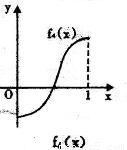
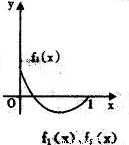
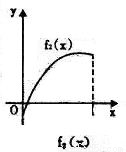
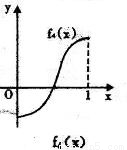
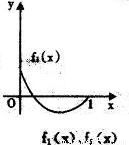
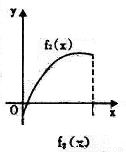
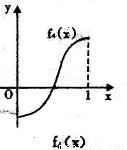
11、如图所示,fi(x)(i=1,2,3,4)是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立”的只有( )
分析:由题设对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立,知,此函数必为一凸函数,依据凸函数的图象特征进行判断即可.
解答:解:由题意,观察四个选项:A选项中的图象先降后升是一凸函数,B选项中的函数是先升后降是一凹函数,C选项中的图象中列出了一部分,不合定义域,D选项中的函数图象凸、凹函数各一部分.
考察定义:对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立知,此函数在[0,1]是凸函数,由上分析知只有A选项符合题意,
故选A.
考察定义:对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立知,此函数在[0,1]是凸函数,由上分析知只有A选项符合题意,
故选A.
点评:本题的考点是函数的图象,考查函数图象的变化规律,在本题中给出了一个新定义,对于新定义的题型,要认真研究其运算特征,充分理解其内涵再依据新规则做题.

练习册系列答案
相关题目