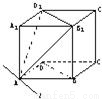
题目内容
已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线,下列结论错误的是
- A.D1B1∥l
- B.BD∥平面AD1B1
- C.l∥平面A1D1B1
- D.l⊥B1C1
D
分析:先根据题意画出图形,再证明由D1B1∥BD,证明D1B1∥平面ABCD,再由线面平行的性质定理证明D1B1∥l.再根据直线与平面平行的判定定理得l∥平面A1D1B1,和BD∥平面AD1B1,对于选项D,可通过反面进行论证.
解答: 解:在正方体ABCD-A1B1C1D1中,D1B1∥BD,
解:在正方体ABCD-A1B1C1D1中,D1B1∥BD,
∵BD?平面ABCD,D1B1?平面ABCD
∴D1B1∥平面ABCD.
又∵平面ABCD∩平面AD1B1=l,
∴D1B1∥l.故A正确;
∵D1B1?平面A1D1B1,∴l∥平面A1D1B1,选项C正确;
∵BD∥D1B1,D1B1?平面AD1B1,∴BD∥平面AD1B1,故B正确.
从而选D.
故选D.
点评:本题考查了平行判定与性质定理的应用,用于线线平行于线面平行的转化,属于基础题.
分析:先根据题意画出图形,再证明由D1B1∥BD,证明D1B1∥平面ABCD,再由线面平行的性质定理证明D1B1∥l.再根据直线与平面平行的判定定理得l∥平面A1D1B1,和BD∥平面AD1B1,对于选项D,可通过反面进行论证.
解答:
 解:在正方体ABCD-A1B1C1D1中,D1B1∥BD,
解:在正方体ABCD-A1B1C1D1中,D1B1∥BD,∵BD?平面ABCD,D1B1?平面ABCD
∴D1B1∥平面ABCD.
又∵平面ABCD∩平面AD1B1=l,
∴D1B1∥l.故A正确;
∵D1B1?平面A1D1B1,∴l∥平面A1D1B1,选项C正确;
∵BD∥D1B1,D1B1?平面AD1B1,∴BD∥平面AD1B1,故B正确.
从而选D.
故选D.
点评:本题考查了平行判定与性质定理的应用,用于线线平行于线面平行的转化,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
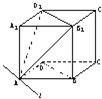 已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线.
已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线. 已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线.
已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线.