题目内容
已知函数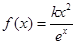 ,其中
,其中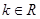 且
且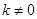 .
.
(I)求函数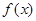 的单调区间;
的单调区间;
(II)当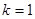 时,若存在
时,若存在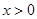 ,使
,使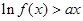 成立,求实数
成立,求实数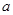 的取值范围.
的取值范围.
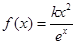 ,其中
,其中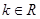 且
且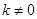 .
.(I)求函数
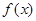 的单调区间;
的单调区间;(II)当
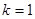 时,若存在
时,若存在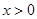 ,使
,使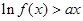 成立,求实数
成立,求实数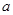 的取值范围.
的取值范围.(I)减区间是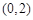 ,增区间是
,增区间是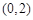 ;(II)
;(II) .
.
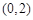 ,增区间是
,增区间是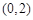 ;(II)
;(II) .
.试题分析:(I)先对函数求导,再分k>0和k<0两种情况讨论,可得函数
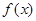 的单调区间;(II)
的单调区间;(II)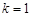 时,
时,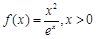 ,由
,由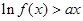 得:
得: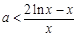 ,构造新函数
,构造新函数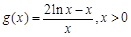 ,对新函数求导得
,对新函数求导得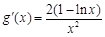 ,判断函数
,判断函数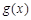 的单调性,就可得
的单调性,就可得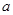 的取值范围.
的取值范围.试题解析:(I)定义域为R,
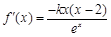 2分
2分当
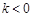 时,
时, 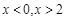 时,
时,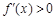 ;
;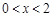 时,
时,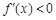
当时,
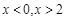 时,
时,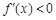 ;
;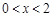 时,
时,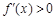 4分
4分所以当
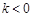 时,
时,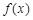 的增区间是
的增区间是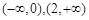 ,减区间是
,减区间是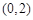
当
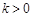 时,
时,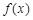 的ug减区间是
的ug减区间是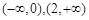 ,增区间是
,增区间是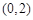 6分
6分(II)
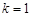 时,
时,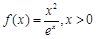 ,由
,由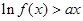 得:
得: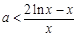
设
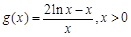 ,
,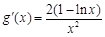 , 8分
, 8分所以当
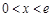 时,
时,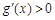 ;当
;当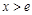 时,
时,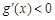 ,
,所以
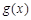 在
在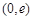 上递增, 在
上递增, 在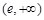 上递减, 10分
上递减, 10分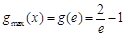 所以
所以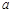 的取值范围是
的取值范围是 12分
12分
练习册系列答案
相关题目
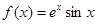 .
.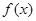 的单调区间;
的单调区间;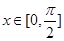 ,
,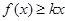 总成立,求实数
总成立,求实数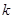 的取值范围;
的取值范围;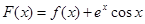 ,
,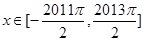 ,过点
,过点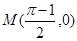 作函数
作函数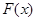 图象的所有切线,令各切点得横坐标构成数列
图象的所有切线,令各切点得横坐标构成数列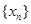 ,求数列
,求数列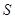 的值.
的值.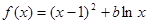 ,其中
,其中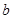 为常数。
为常数。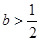 时,判断函数
时,判断函数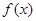 在定义域上的单调性;
在定义域上的单调性;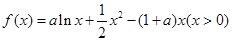 .
.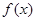 的单调区间;
的单调区间;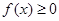 在
在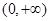 内恒成立,求实数
内恒成立,求实数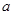 的取值范围.
的取值范围.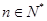 ,求证:
,求证: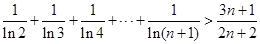 .
.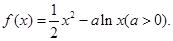
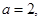 求
求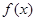 在
在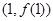 处的切线方程;
处的切线方程;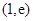 上恰有两个零点,求
上恰有两个零点,求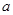 的取值范围.
的取值范围.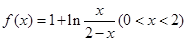 .
.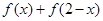 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;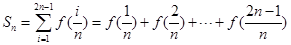 ,其中
,其中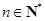 ,求
,求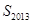 ;
;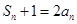 .若不等式
.若不等式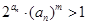 对
对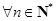 且
且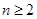 恒成立,求实数
恒成立,求实数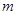 的取值范围.
的取值范围.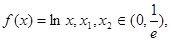 且
且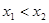 则下列结论正确的是( )
则下列结论正确的是( )



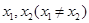 是函数
是函数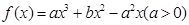 的两个极值点.
的两个极值点.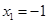 ,
,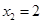 ,求函数
,求函数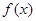 的解析式;
的解析式;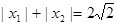 ,求实数
,求实数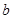 的最大值;
的最大值;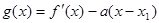 ,若
,若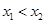 ,且
,且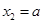 ,求函数
,求函数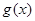 在
在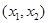 内的最小值.(用
内的最小值.(用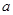 表示)
表示)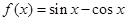 且
且 是f(x)的导函数,若
是f(x)的导函数,若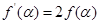 ,,则
,,则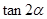 = .
= .