题目内容
在△ABC中,有下列命题:
①A>B的充要条件为sinA>sinB; ②A<B的充要条件为cosA>cosB;
③若A,B为锐角,则sinA+sinB>cosA+cosB; ④tan
tan
为常数.
其中正确的命题的个数为( )
①A>B的充要条件为sinA>sinB; ②A<B的充要条件为cosA>cosB;
③若A,B为锐角,则sinA+sinB>cosA+cosB; ④tan
| A+B |
| 2 |
| C |
| 2 |
其中正确的命题的个数为( )
分析:由题意,可借助三角函数的相关公式对四个命题 真假性作出判断
①命题判断可分两类,角A是钝角与不是钝角两类证明;②命题可由余弦函数在(0,π)上是减函数得出命题是真命题;③命题可由角C的取值未定,无法得了A,B两角和的范围,真假性无法判断;④命题可由两角和为
,故两角正切值互为倒数作出判断
①命题判断可分两类,角A是钝角与不是钝角两类证明;②命题可由余弦函数在(0,π)上是减函数得出命题是真命题;③命题可由角C的取值未定,无法得了A,B两角和的范围,真假性无法判断;④命题可由两角和为
| π |
| 2 |
解答:解:在△ABC中,
①A>B的充要条件为sinA>sinB;此是一个真命题,若A>B,当A不超过90°时,显然可得出sinA>sinB,当A是钝角时,由于
>π-A>B,可得sin(π-A)=sinA>sinB,即 A>B是sinA>sinB的充分条件,当sinA>sinB时,亦可得 A>B,由此知 A>B的充要条件为sinA>sinB
②A<B的充要条件为cosA>cosB;上命题是真命题,由于余弦函数在(0,π)上是减函数,故A<B的充要条件为cosA>cosB;
③若A,B为锐角,则sinA+sinB>cosA+cosB;此命题是假命题,由于角C的范围不确定,无法判断sinA+sinB>cosA+cosB是否成立;
④tan
tan
为常数,此命题正确,由于
+
=
,可得tan
tan
为常数
综上知①②④是正确命题
故选C
①A>B的充要条件为sinA>sinB;此是一个真命题,若A>B,当A不超过90°时,显然可得出sinA>sinB,当A是钝角时,由于
| π |
| 2 |
②A<B的充要条件为cosA>cosB;上命题是真命题,由于余弦函数在(0,π)上是减函数,故A<B的充要条件为cosA>cosB;
③若A,B为锐角,则sinA+sinB>cosA+cosB;此命题是假命题,由于角C的范围不确定,无法判断sinA+sinB>cosA+cosB是否成立;
④tan
| A+B |
| 2 |
| C |
| 2 |
| A+B |
| 2 |
| C |
| 2 |
| π |
| 2 |
| A+B |
| 2 |
| C |
| 2 |
综上知①②④是正确命题
故选C
点评:本题的考点是命题的真假判断与应用,考查了充要条件的判断,正、余弦函数大小的比较等,解题的关键是理解三角函数的性质,灵活运用三角函数的性质作出判断,本题考查了判断推理的能力及分类讨论的思想

练习册系列答案
相关题目
 tan
tan 为常数.
为常数.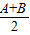 tan
tan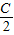 为常数.
为常数.