题目内容
设曲线y=![]() 和曲线y=
和曲线y=![]() 在它们的交点处的两切线的夹角为α,求tanα的值.
在它们的交点处的两切线的夹角为α,求tanα的值.
答案:
解析:
解析:
|
解:联立两曲线方程 设两曲线在交点处的切线斜率分别为k1、k2,则 ∴k1=( 由两直线夹角公式:tanα=| 分析:要求两切线的夹角,关键是确定在两曲线交点处的切线的斜率.根据导数的几何意义,只需先求出两曲线在交点处的导数,再应用两直线夹角公式求出夹角即可. |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
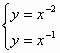 解得两曲线交点为(1,1).
解得两曲线交点为(1,1). -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0, (x>0),
(x>0), ,又a<0,
,又a<0,